3.1 Математична пам’ятка

3.1.1 Дроби

Серед дробів можна виділити наступні закономірності:

\[a+\frac{c}{d} = \frac{ad+c}{d}\]

\[\frac{a}{b}+\frac{c}{d} = \frac{ad+cb}{bd}\]

\[\frac{a}{b} - \frac{c}{d} = \frac{ad-cb}{bd}\]

\[\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}\]

\[\frac{a/b}{c/d} = \frac{a}{b} \cdot \frac{d}{c}\]

\[\text{якщо } \frac{a}{b} = \frac{c}{d} \text{, то } \frac{a}{b} = \frac{c}{d} = \frac{a+b}{c+d}\]

3.1.2 Математичні символи

На цьому етапі варто ввести також декілька позначень, які можуть бути маловідомими, наприклад,

• \(>, \geq, <, \leq\) : більше, більше або дорівнює, менше, менше або дорівнює;
• \(\subset, \not\subset\) : є або не є підмножиною;
• \(\in, \notin\) : в або не в;
• \(\{x : x > a\}\) : множина таких \(x\), що для кожного \(x\) в цій множині \(x>a\);
• \(A^c\) - комплемент до множини \(A\), сукупність елементів які не належать до \(A\): \(\{x: x \notin A\}\);
• \(\emptyset\) - порожня множина, в якій нічого нема.
• \((a, b) = \{x:a<x<b\}\),
• \([a, b] = \{x:a \leq x \leq b\}\);
• \(\propto\) : пропорційно до;
• \(\simeq\) : приблизно дорівнює;
• \(\sim\) : подібно до, однак часто позначає змінну, що розподілена відповідно до певного розподілу;
• \(\cup\) : об’єднання множин;
• \(\cap\) : перетин множин;
• \(\exists\) : існує;
• \(\Rightarrow\) : відтак;
• \(\iff\) : рівнозначно;
• \(\forall\) : для всіх;
• \(\sum\limits_{i=j}^{n}x_i\) : сума всіх елементів \(x_i\) де \(i = j, j+1, j+2, \cdots, n-2, n-1, n\);
• \(\prod\limits_{i=j}^{n}x_i\) : добуток всіх елементів \(x_i\) де \(i = j, j+1, j+2, \cdots, n-2, n-1, n\);
• \(a!\) є факторіалом, де \(a! = 1 \cdot 2 \cdot 3 \cdot \cdots \cdot (a-2) \cdot (a-1) \cdot a\);
• \(\binom{a}{b}\) є біноміальним коефіцієнтом, де \(\binom{a}{b} = \frac{a!}{b!(a-b)!}\).

3.1.3 Нерівності

Перелічені символи можна використати для пояснення нерівностей, зокрема,

\[a < b, c \leq d \Rightarrow \begin{cases} a + c < b + d\\ a + c < b + c\\ a - c < b - c \end{cases}\]

\[a < b, c > 0 \Rightarrow \begin{cases} ac < bc\\ \frac{a}{c} < \frac{b}{c} \end{cases}\]

\[a < b, c < 0 \Rightarrow \begin{cases} ac > bc\\ \frac{a}{c} > \frac{b}{c}\\ -a > -b \end{cases}\]

\[0 < a < b\Rightarrow \frac{1}{a} > \frac{1}{b} > 0\]

\[a < b\Rightarrow \begin{cases} \frac{a+x}{b+x} > \frac{a}{b} \\ \frac{a-x}{b-x} < \frac{a}{b} \end{cases}\]

\[a > b\Rightarrow \begin{cases} \frac{a+x}{b+x} < \frac{a}{b} \\ \frac{a-x}{b-x} > \frac{a}{b} \end{cases}\]

3.1.4 Ступені

Класичне визначення ступеню наступне:

\[a^b = \underbrace{a \cdot a \cdot a \cdot \cdots \cdot a}_b\] або, в нотації добутку¹³,

\[a^b = \prod\limits_{i=1}^b a\]

Для ступенів властиво наступне:

\[a^0 = 1\]

\[a^1 = a\]

\[a^{-m} = \frac{1}{a^m}\]

\[a^m \times a^n = a^{m+n}\]

\[\frac{a^m}{a^n} = a^{m-n}\]

\[(a^m)^n = a^{m \cdot n}\]

\[a^n \cdot b^n = (ab)^n\]

\[\frac{a^n}{b^n} = \left( \frac{a}{b}\right)^n\]

\[a^{\frac{m}{n}} = \sqrt[\leftroot{5} \uproot{10} n]{a^m} \Rightarrow a^{1/2} = \sqrt{a}\]

\[\frac{\sqrt[\leftroot{5} \uproot{10} n]{a}}{\sqrt[\leftroot{5} \uproot{10} n]{b}} = \sqrt[\leftroot{5} \uproot{10} n]{\frac{a}{b}} \iff \frac{\sqrt[\leftroot{5} \uproot{10} n]{a}}{\sqrt[\leftroot{5} \uproot{10} n]{b}} = \frac{a^{1/n}}{b^{1/n}} = \left( \frac{a}{b} \right)^{1/n}\]

Зведення константи в змінний ступінь (експонента) іноді може позначатись дещо незвично:

\[\exp (x_i) = e^{x_i}\]

де \(e\) – число Ейлера.

В комп’ютерних системах можна також зустріти позначення на кшталт 1e-07. В цьому випадку мається на увазі експоненціювання за основою \(10\):

\[\text{1e-07} = 1 \cdot 10^{-7}\]

3.1.5 Ряди чисел

Прогресії є рядами чисел, котрі підпорядковуються певним законам. Наприклад,

• арифметична прогресія має вигляд \(a, a+d, a+2d, a+3d, \cdots\), де \(n\)-ний член має значення \(T_n = a + (n-1)d\), а сума перших \(n\) членів складає

\[S_n = \sum\limits_{i=1}^n T_n = \sum\limits_{i=1}^n \left[ a + (i-1)d \right] = \frac{n}{2}[2a+(n-1)d]\]

• геометрична прогресія має вигляд \(a, ar, ar^2, ar^3, \cdots\), де \(n\)-ний член має значення \(T_n = ar^{n-1}\), а сума перших \(n\) членів складає

\[S_n = \sum\limits_{i=1}^n ar^{i-1} = \begin{cases} a \left( \frac{r^n - 1}{r-1} \right) \text{ якщо } r<1 \\ a \left( \frac{1-r^n}{1-r} \right) \text{ якщо } r>1 \end{cases}\]

Суму перших \(n\) натуральних чисел можна розрахувати як

\[1+2+3+\cdots + n = \sum\limits_{i=1}^n i = \frac{n(n+1)}{2}\]

Суму квадратів перших \(n\) натуральних чисел можна розрахувати як

\[1^2+2^2+3^2+\cdots + n^2 = \sum\limits_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}\]

Суму кубів перших \(n\) натуральних чисел можна розрахувати як

\[1^3+2^3+3^3+\cdots + n^3 = \sum\limits_{i=1}^n i^3 = \left( \frac{n(n+1)}{2} \right)^2\]

3.1.6 Ступені арифметичних операцій

\[(a+b)^2 = a^2 + 2ab + b^2\]

\[(a-b)^2 = a^2 - 2ab + b^2\]

\[(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\]

\[(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3\]

\[a^2 - b^2 = (a^2 - b^2)(a^2 + b^2)\]

\[a^3 + b^3 = (a+b)(a^2 - ab + b^2)\]

\[a^3 - b^3 = (a-b)(a^2 + ab + b^2)\]

3.1.7 Лінійні та поліноміальні функції

Лінійні рівняння мають чимале значення в популярних статистичних методах, зокрема, лінійній регресії. Найпростішу лінійну функцію можна розглядати як пряму горизонтальну лінію, котра ніяк не залежить від предиктора \(x\) (Рис. 3.1):

\[y = f(x) = a\]

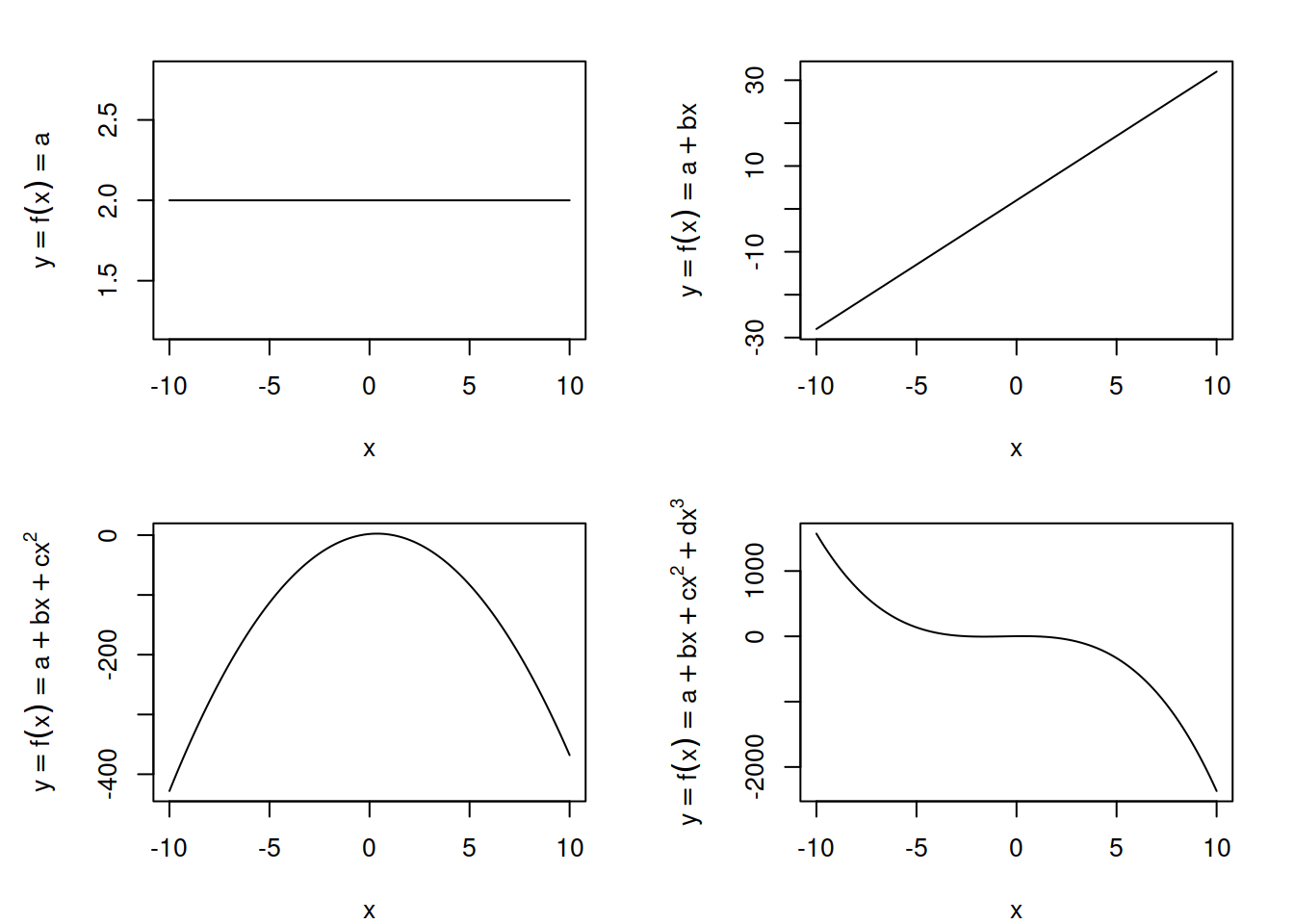
Рис. 3.1: Лінійні та поліноміальні функції \(y = f(x)\) де \(f(x) = a\), \(f(x) = a + bx\), \(f(x) = a + bx + cx^2\), \(f(x) = a + bx + cx^2 + dx^3\) для \(a=2, b = 3, c = -4, d = -2\).

Більш поширеними є рівняння прямих ліній, які залежать від змінної \(x\). Найпростішим прикладом буде лінійне рівняння вигляду

\[y = f(x) = a + bx\]

де коефіцієнт \(a\) відповідає значенню \(y\) за \(x = 0\) та коефіцієнт \(b\) відповідає нахилу прямої, тобто відповідає на питання “на скільки одиниць змінюється \(y\) за зміни \(x\) на одну одиницю”.

Наприклад, розгляньмо детальніше функцію \(y = f(x) = a + bx\), в якій \(a = 2, b = 3\) (Рис. 3.2):

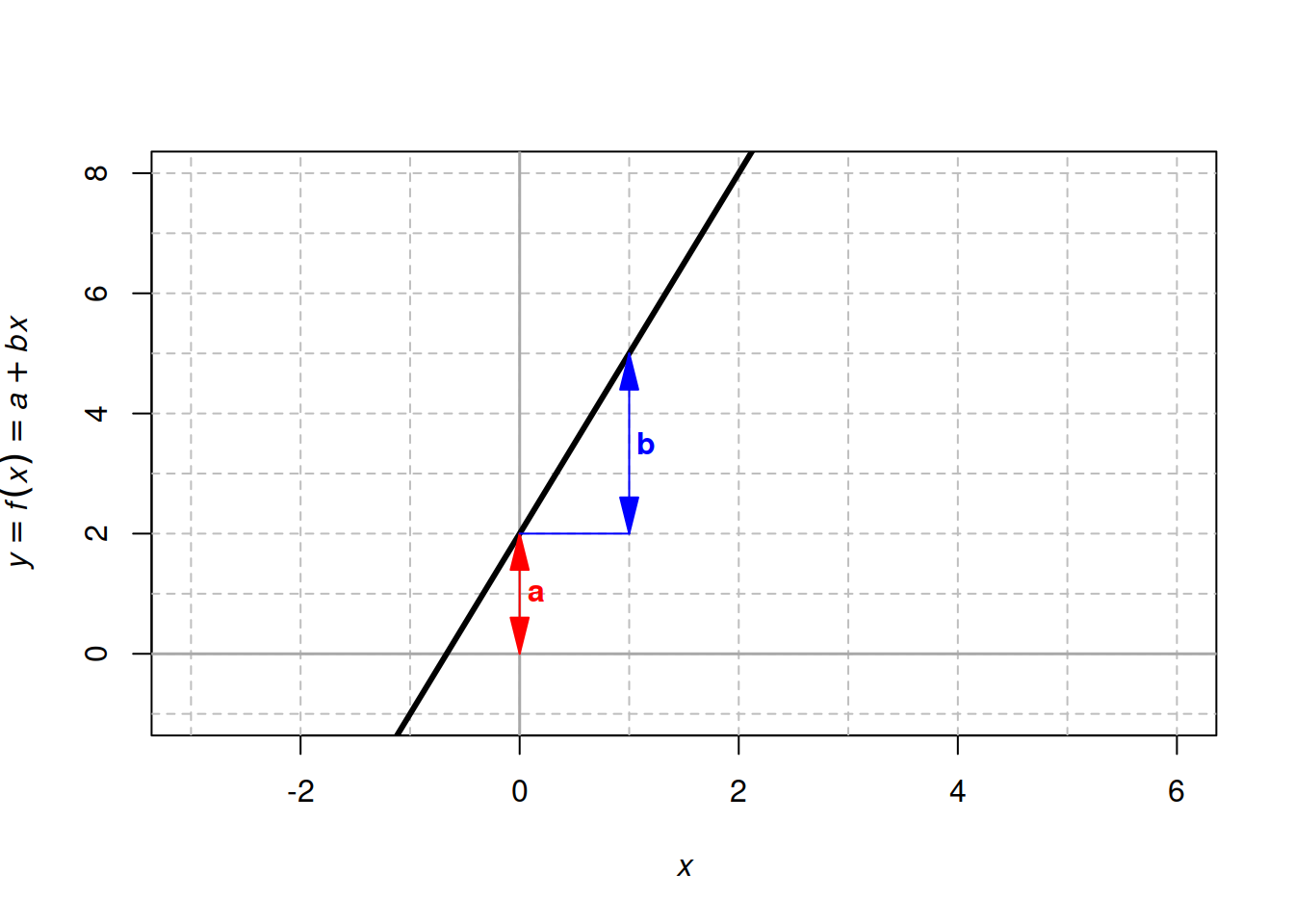
Рис. 3.2: Зміст параметрів лінійної функції \(y = f(x) = a + bx\) для \(a=2, b = 3\).

Лінійна функція є окремим випадком поліноміальної функції, в якій ми буквенні коефіцієнти (\(a, b, c, \cdots\)) позначимо через індексовані коефіцієнти (\(\beta_0, \beta_1, \beta_2, \cdots\)):

\[p(x, m) = \beta_0 + \beta_1 x + \beta_2 x^2 + \cdots + \beta_m x^m\]

де \(m\) позначає ступінь полінома. Відтак, найпростіша функція перетину є поліноміальною функцією ступеню \(m = 0\), де \(p(x, m = 0) = \beta_0\), функція прямої є поліноміальною функцією ступеню \(m = 1\), де \(p(x, m = 1) = \beta_0 + \beta_1 x\), квадратична функція є поліноміальною ступеню \(m = 2\), де \(p(x, m = 2) = \beta_0 + \beta_1 x + \beta_2 x^2\) тощо.

Варто зазначити, що \(y\) може бути не лише лінійною функцією однієї змінної, скажімо, \(x\), а й комбінації \(m\) змінних \((x_1, x_2, x_3, \cdots, x_m)\), наприклад,

\[y = f(x_1, x_2, \cdots, x_m) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_m x_m\]

В статистичному методі лінійної регресії одна зі змінних може являти собою трансформовану іншу змінну. Наприклад, якщо ми визначимо \(x_2\) як \(x_2 = (x_1)^2\), то квадратне рівняння можна визначити як лінійну комбінацію:

\[y = f(x_1, x_2) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 = \beta_0 + \beta_1 x_1 + \beta_2 (x_1^2) = p(x_1, 2)\]

Таким чином, лінійна регресія може бути легко використана для моделювання нелінійних поліноміальних взаємозв’язків за рахунок трансформації змінних і їх використання в лінійних рівняннях.

3.1.8 Логарифми

Логарифмування є зворотним процесом то зведення в ступінь. Логарифм числа \(x\) із основою \(a\) є таким числом, зведення якого до ступеню \(a\) поверне число \(x\), тобто,

\[\log_a x = b\iff a^b = x\]

Найбільш поширеними є десятковий логарифм \(\log_{10}\) та натуральний логарифм \(\log_e\) де \(e\) – число Ейлера \(e \approx 2.718\), константа, визначена як \(e = \lim\limits_{n \rightarrow \infty} (1 + \frac{1}{n})^n\).

В екології особливо поширений модифікований десятковий логарифм, оскільки чисельності організмів часто мають або низькі значення на кшталт \(0, 1, 2\), або дуже високі значення порядку сотень та тисяч, на рівні яких можна знехтувати одиничними особами¹⁴.

Модифікація логарифмічної трансформації в екології побудована таким чином, аби \(0\) відповідало \(0\) особин, \(1\) відповідало \(1\) особині, \(2\) відповідало \(10\) особинам, \(3\) відповідало \(100\) особинам, і так далі (Anderson et al. 2006). Такої трансформації легко досягнути використовуючи функцію котра враховує факт, що логарифмування від’ємних значень та нуля неможливе (\(\log0 = -\infty\)):

\[f(x) = \begin{cases} [\log_{10}(x)+1] \times \mathbb{I}_x(x > 0)\\ 0 \times \mathbb{I}_x(x = 0) \end{cases}\]

де \(\mathbb{I}_x(\cdot)\) є індикаторною функцією, котра приймає значення \(1\) якщо логічна умова \((\cdot)\) (тут, що \(x > 0\)) справджується.

Варто мати на увазі, що, в загальному, логарифмічне трансформування чисельностей не є оптимальною практикою, адже різниця між \(\log_{10}(0)\) та \(\log_{10}(1)\) така ж, як, наприклад, між \(\log_{10}(1000)\) та \(\log_{10}(10000)\), в той час як відсутність виду, котра призводить до отримання нульової чисельності, може передбачати набагато важливіші екологічні механізми порівняно із присутністю виду, котра призводить до не-нульової чисельності (O’Hara and Kotze 2010).

Логарифми мають наступні властивості:

\[\log_a(xy) = \log_a(x) + \log_a(y)\]

\[\log_a(\frac{x}{y}) = \log_a(x) - \log_a(y)\]

\[\log_a(x^b) = b \log_a (x)\]

\[\log_a(x) = \frac{\log_b (x)}{\log_b (a)} \forall b\]

3.1.9 Поширені математичні функції

Кількість найпростіших математичних функцій доволі обмежена, однак, їх використання для трансформації змінних може бути кардинально різним. Трансформація даних може знадобитись пізніше, наприклад, для задоволення передбачень певних статистичних методів. Наприклад, лінійна регресія передбачає, що змінні розподілені нормально. В разі, якщо це не відповідає дійсності, одним із варіантів подальших дій є трансформування змінних певною функцією (наприклад, логарифмічно), за чого результуюча змінна може мати ближчий до нормального розподіл. Форми таких функцій наведені на Рис. 3.3.

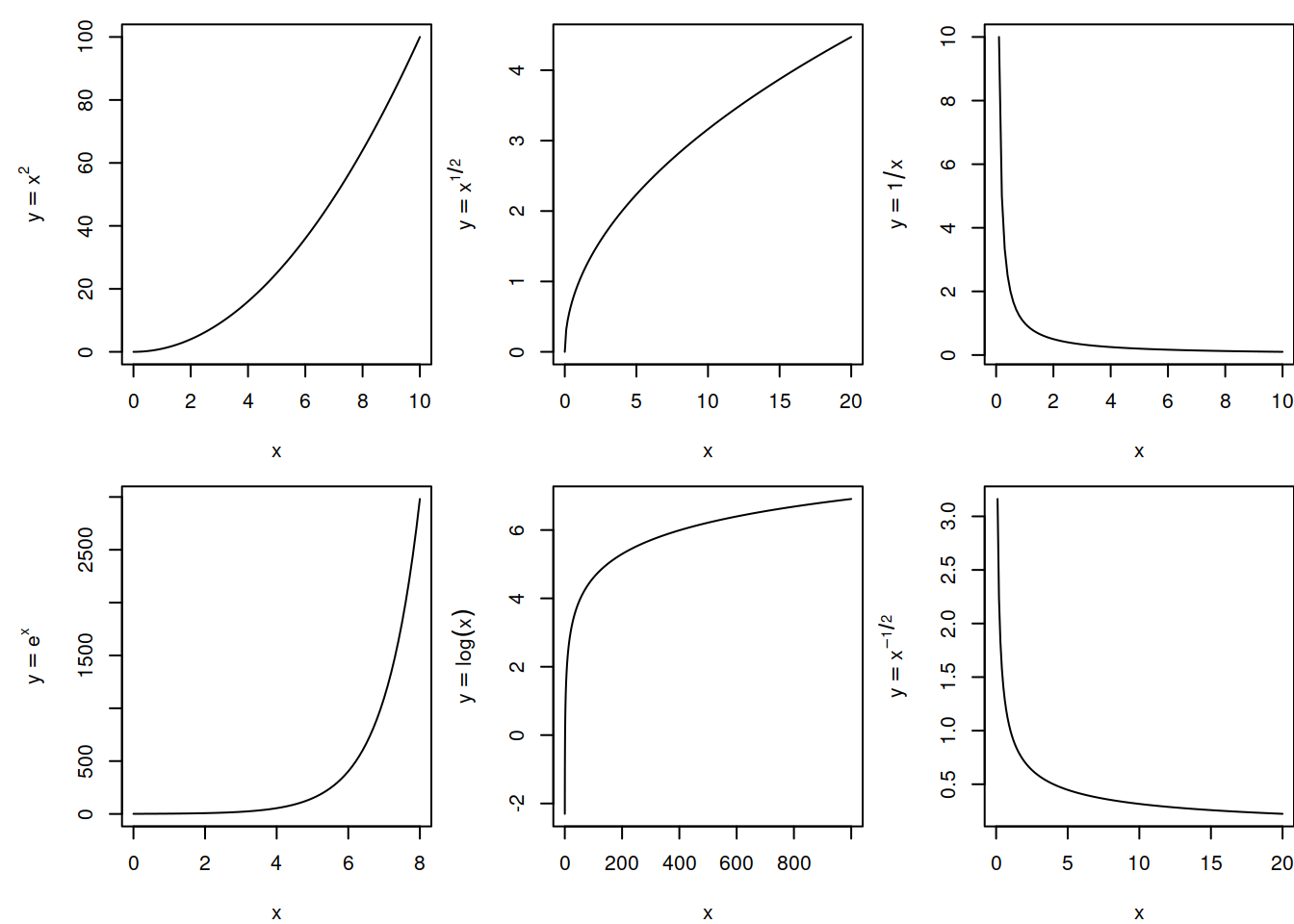
Рис. 3.3: Графіки поширених функцій.

Варто також мати на увазі зворотні функції:

• поліноми та корені \(f(x) = x^2 \iff f^{-1}(y) = y^{1/2}\);
• експоненти та логарифми \(f(x) = e^x \iff f^{-1}(y) = \log_e(y)\);
• зворотні функції \(f(x) = 1/x \iff f^{-1}(y) = 1/y\).

3.1.10 Властивості сум

Суму позначають як \(\sum\limits_{i=m}^{n}f(x_i)\) де \(i\) є індексом сумації, \(x_i\) – індексованою змінною, \(m\) – нижня межа сумації, \(n\) – верхня межа сумації. В програмуванні таку нотацію можна пояснити через цикл:

sum(for (i in m:n){
  f(x[i])
})

Суми мають наступні властивості

\[\sum\limits_{i=m}^{n}c\cdot f(x_i) = c \cdot \sum\limits_{i=m}^{n} f(x_i) \text{ } \forall \text{ } c : \text{const}\]

\[\sum\limits_{i=m}^{n} \left[ f(x_i) + g(x_i)\right] = \sum\limits_{i=m}^{n} f(x_i) + \sum\limits_{i=m}^{n} g(x_i)\]

\[\sum\limits_{i=m}^{n} f(x_i) = \sum\limits_{i=m}^{a} f(x_i) + \sum\limits_{i=a+1}^{n} f(x_i)\]

\[\left( \sum\limits_{i = m}^n x_i \right)\left( \sum\limits_{j = m}^n y_j \right) = \sum\limits_{i = m}^n \sum\limits_{j = m}^n (x_i y_j)\]

\[\sum \limits_{i=1}^n c = nc\]

\[\sum \limits_{i=0}^n \log i = \log n!\]

\[\sum \limits_{i=0}^n \binom{n}{i} = 2^n\]

\[\sum \limits_{i=0}^n \binom{n}{i} a^{n-i} b^i = (a+b)^n\]

3.1.11 Властивості добутків

Зміст нотації добутків подібний до суми. Суму позначають як \(\prod\limits_{i=m}^{n}f(x_i)\) де \(i\) є індексом добутку, \(x_i\) – індексованою змінною, \(m\) – нижня межа добутку, \(n\) – верхня межа добутку. Для добутків притаманні наступні властивості:

\[\prod\limits_{i=1}^n x = x^n\]

\[\prod\limits_{i=1}^n x_i y_i = \left( \prod\limits_{i=1}^n x_i\right)\left( \prod\limits_{i=1}^n y_i\right)\]

\[\left( \prod\limits_{i=1}^n x_i \right)^a = \prod\limits_{i=1}^n x_i^a\]

\[\log_b \left[ \prod\limits_{i = m}^n f(x_i) \right] = \sum\limits_{i=m}^n \left[ \log_b f(x_i) \right]\]

\[\prod\limits_{i = m}^n [c \cdot f(x_i)] = c^{\sum_{i=m}^n f(x_i)}\]

3.1.12 Диференціювання

Диференціювання функції – це процес знаходження похідної цієї функції. Похідна функції \(f(x)\) є такою функцією \(f'(x)\), котра описує зміну значення \(f(x)\) за зміни значення аргументу \(x\).

Наприклад, на Рис. 3.2 зображено функцію прямої лінії \(f(x) = 2 + 3x\). В цьому випадку, приріст функції становить 3 одиниці \(y\) на одну одиницю \(x\), і цей приріст залишається незмінним за будь-якого значення \(x\), оскільки функція є прямою. Цей приріст і є похідною, отже, \(f'(x) = 3\).

А що щодо випадків, коли \(f(x)\) не є лінійною, що трапляється набагато частіше? В такому випадку, приріст \(f(x)\) залежить від значення \(x\), тобто \(f'(x)\) теж є функцією із аргументом \(x\). Власне, знаходження цієї функції і є метою диференціювання. Формально, визначення похідної являє собою зміну \(f(x)\) за найменшої різниці \(x\).

Наприклад, визначмо функцію \(f(x) = -5x + x^3\) (Рис. 3.4):

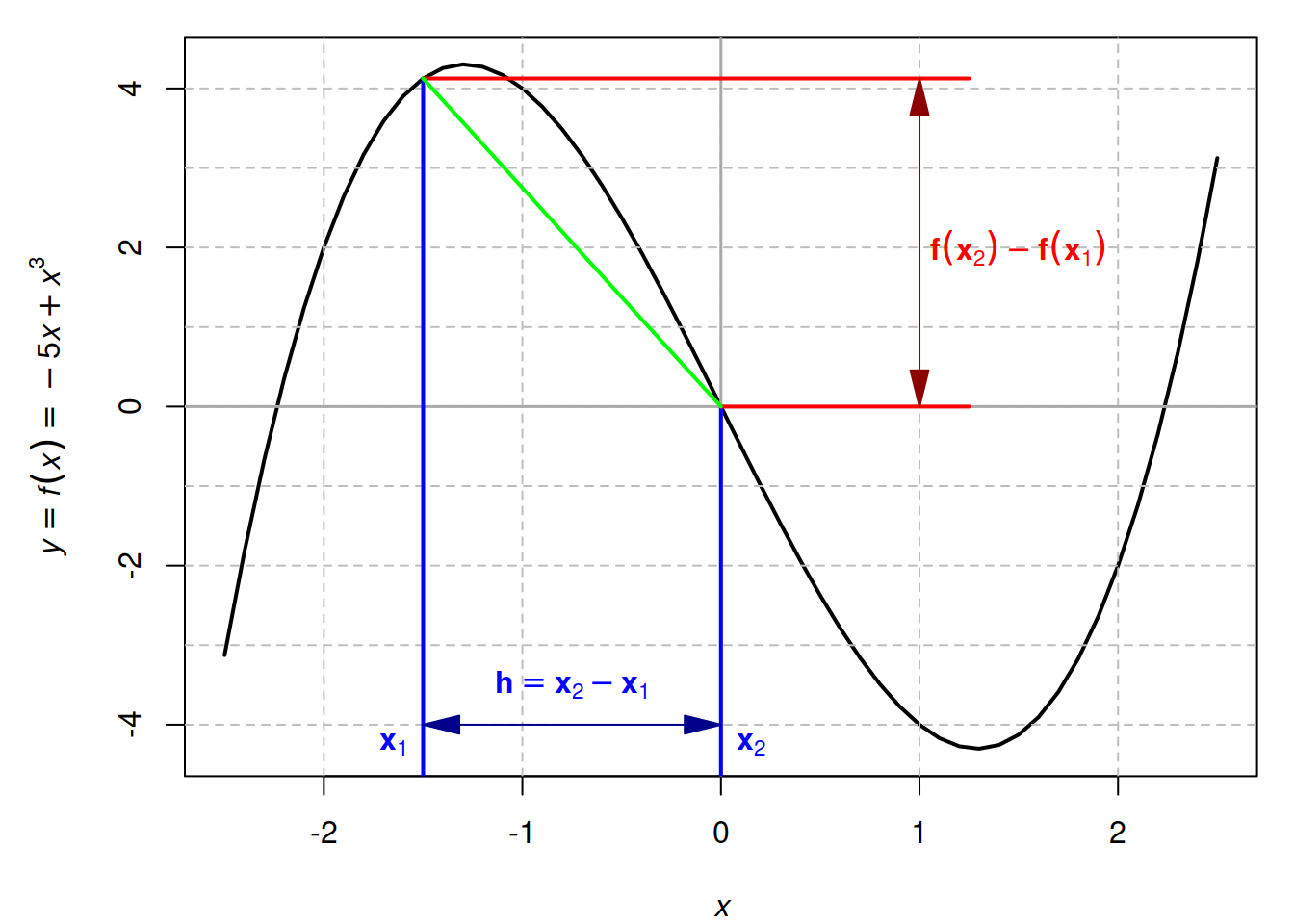
Рис. 3.4: Функція \(f(x) = -5x + x^3\). Приріст цієї функції між \(x_1\) та \(x_2 = x_1 + h\) складає \(\frac{f(x_1 + h) - f(x_1)}{h}\).

Для цієї функції, похідна буде такою функцією із аргументом \(x\), котра описуватиме \(f(x_2) - f(x_1)\) на зміну \((x_2 - x_1)\). На Рис. 3.4 показано зміну \(f(x)\) для \(x_2 = 0, x_1 = -1.5\), тобто \(h = x_2 - x_1 = 1.5\), де значення функції становить \(f(x_2) = -5 \cdot 0 + 0^3 = 0\), \(f(x_1) = -5 \cdot (-1.5) + (-1.5)^3 = 4.125\), отже, \(f(x_2) - f(x_1) = f(x_1+h) - f(x_1) = -4.125\), а темп цієї зміни на одиницю \(x\) становить \(\frac{f(x_1 + h) - f(x_1)}{h} = \frac{-4.125}{1.5} = -2.75\).

На тій частині функції, котра відповідає \(x_1, x_1+h\), отримане значення темпу зміни може не цілком відповідати реальній картині. Ми бачимо, що функція трішки зростає після \(x_1\), потім спадає, і взагалі є нелінійною, але обчислене значення \(\frac{f(x_1 + h) - f(x_1)}{h} = \frac{-4.125}{1.5} = 2.75\) відповідає ситуації, коли розглянута функція є прямою лінією (зображено зеленим). Аби відобразити справжню природу зміни значення функції, необхідно зменшити значення \(h\) до найменшого можливого значення. Відтак, класичне визначення похідної – це така функція із аргументом \(x\), що описує темп зміни \(\frac{f(x+h) - f(x)}{h}\) за найменшої зміни \(h\):

\[f'(x) = \frac{df(x)}{dx} = \lim\limits_{h \rightarrow 0}\frac{f(x+h) - f(x)}{h}\]

де позначення похідної через \(\frac{df(x)}{dx}\) інтуїтивно вказує на її природу, якщо позначити зміну значення змінної через \(d\): зміна значення \(f(x)\) поділена на зміну значення \(x\). Похідну варто сприймати як приріст функції, котрий буде позитивним коли функція зростає, негативним коли функція спадає, і дорівнює нулю коли функція залишається сталою (таке можливе або якщо функція є прямою горизонтальною лінією, або коли в точках перегину, коли функція перестає зростати і починає спадати або навпаки).

Похідні мають наступні властивості, котрі допомагають розрахувати їх для будь-якої неперервної функції:

\[\frac{d}{dx}a = 0\]

\[\frac{d}{dx}ax = a\]

\[\frac{d}{dx} x^a = ax^{a-1}\]

\[\frac{d}{dx} e^x = e^x\]

\[\frac{d}{dx} a^x = a^x \ln (a) \text{ } \forall \text{ } a>0\]

\[\frac{d}{dx} \ln (x) = \frac{1}{x} \text{ } \forall \text{ } x>0\]

\[\frac{d}{dx} \log_a(x) = \frac{1}{x \ln(a)}\]

В диференціюванні складних функцій (функцій, котрі складаються з інших функцій, наприклад, \(f(\cdot)\) і \(g(\cdot)\)) керуються наступними правилами:

\[\frac{d}{dx} \left( af(x) + b g(x) \right) = a \frac{d}{dx}f(x) + b \frac{d}{dx}g(x) \iff (af(x) + bg(x))' = af'(x) + bg'(x)\]

\[\frac{d}{dx}(f(x)g(x)) = \frac{df(x)}{dx} g(x) + f(x) \frac{dg(x)}{dx} \iff (f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\]

\[\frac{d}{dx} \left( \frac{f(x)}{g(x)}\right) = \frac{\frac{df(x)}{dx}g(x) - f(x) \frac{dg(x)}{dx}}{g(g(x))} \iff \left( \frac{f(x)}{g(x)} \right)' = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\]

і для функції функції \(f(x) = h(g(x))\),

\[\frac{df(x)}{dx} = \frac{dh(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx} \iff f'(x) = h'(g(x)) \cdot g'(x)\]

Оскільки похідна є функцією сама по собі, її також можна диференціювати (тобто знайти \(n\)-ну похідну, або похідну \(n\)-ного порядку). Наприклад, для функції \(f(x) = -5x + x^3\),

\[\begin{cases} \frac{d}{dx}f(x) = -5 + 3x^2 \\ \frac{d^2}{dx}f(x) = 6x \\ \frac{d^3}{dx}f(x) = 6 \\ \frac{d^4}{dx}f(x) = 0 \end{cases}\]

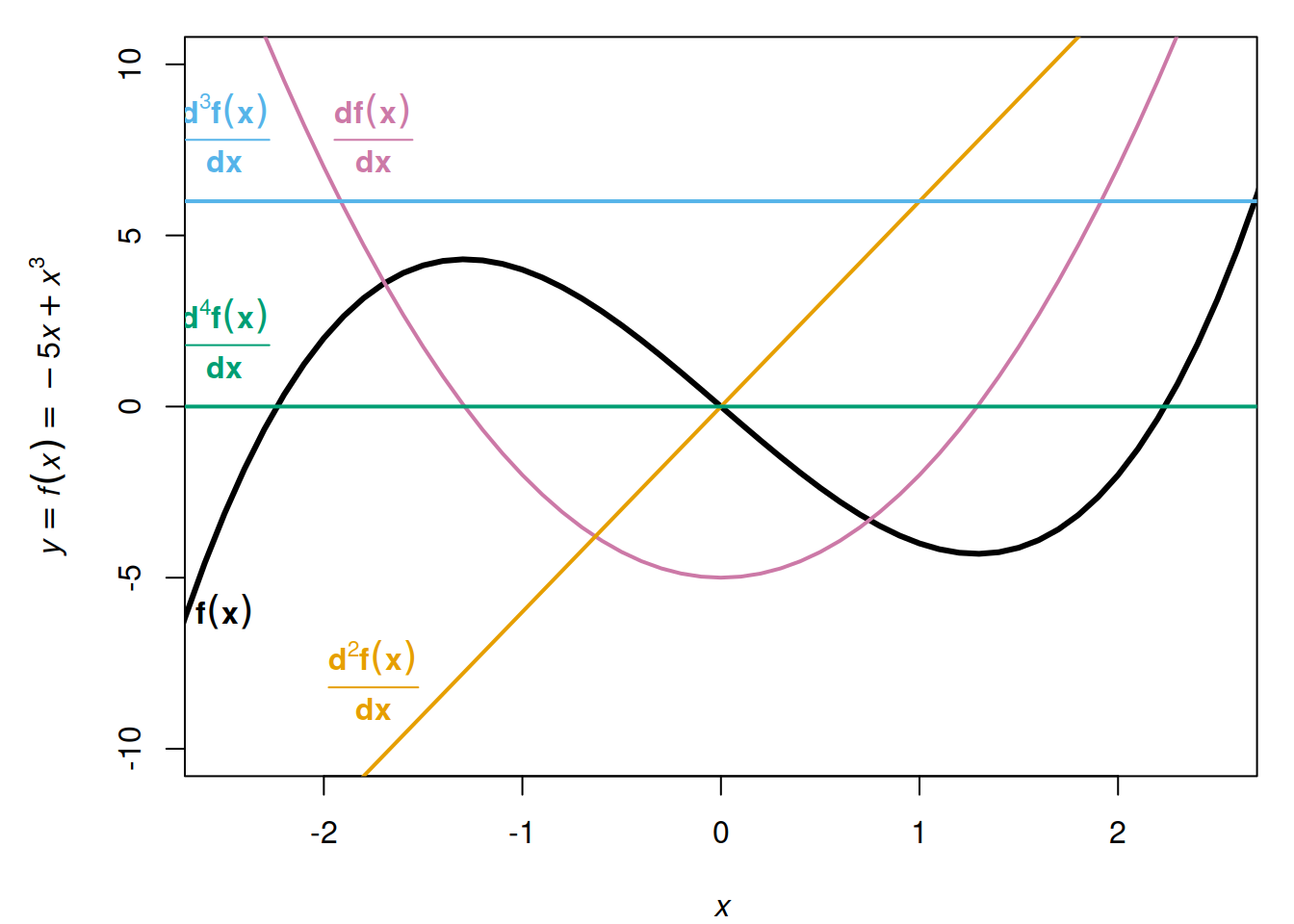
Рис. 3.5: Функція \(f(x) = -5x + x^3\) та її похідні.

3.1.13 Інтегрування

Інтегрування функції \(f(x)\) – це процес знаходження такої функції \(F(x)\), похідна якої являє собою функцію \(f(x)\):

\[\frac{d}{dx}F(x) = f(x) \iff \int f(x) dx = F(x) + C\]

де \(C\) – це будь-яка константа (оскільки похідна константи дорівнює нулю, ця константа не впливає на результат диференціювання).

Інтеграл є, певною мірою, континуальний аналог суми: якщо означення суми оперує дискретними значеннями \(i: i = 1, 2, 3, \cdots, n\), то інтеграл, подібно до похідних, розраховується для найменших можливих інтервалів аргументу функції \(x\).

Невизначений інтеграл функції \(f(x)\) \(\int f(x)dx = F(x)\) має зміст як функція, похідна якої дорівнює вихідній функції \(f(x)\). Водночас, визначений інтеграл \(\int\limits_a^b f(x) dx = F(b) - F(a)\) часто використовується для знаходження площі під кривою \(f(x)\), що обмежена значеннями \(a\) і \(b\).

В разі, якщо аналітичне знаходження невизначеного інтегралу складне або неможливе, корисним може видатись Рейманівське визначення визначеного інтегралу:

\[\int\limits_a^b f(x) dx = F(a) - F(b) = \sum\limits_{i=1}^n [F(x_i) - F(x_{i-1})]\]

де \([F(x_i) - F(x_{i-1})]\) є площею прямокутника, обмеженого функцією \(f(x)\) і дуже маленьким інтервалом \([x_{i-1}, x_i)\) (Рис. 3.6).

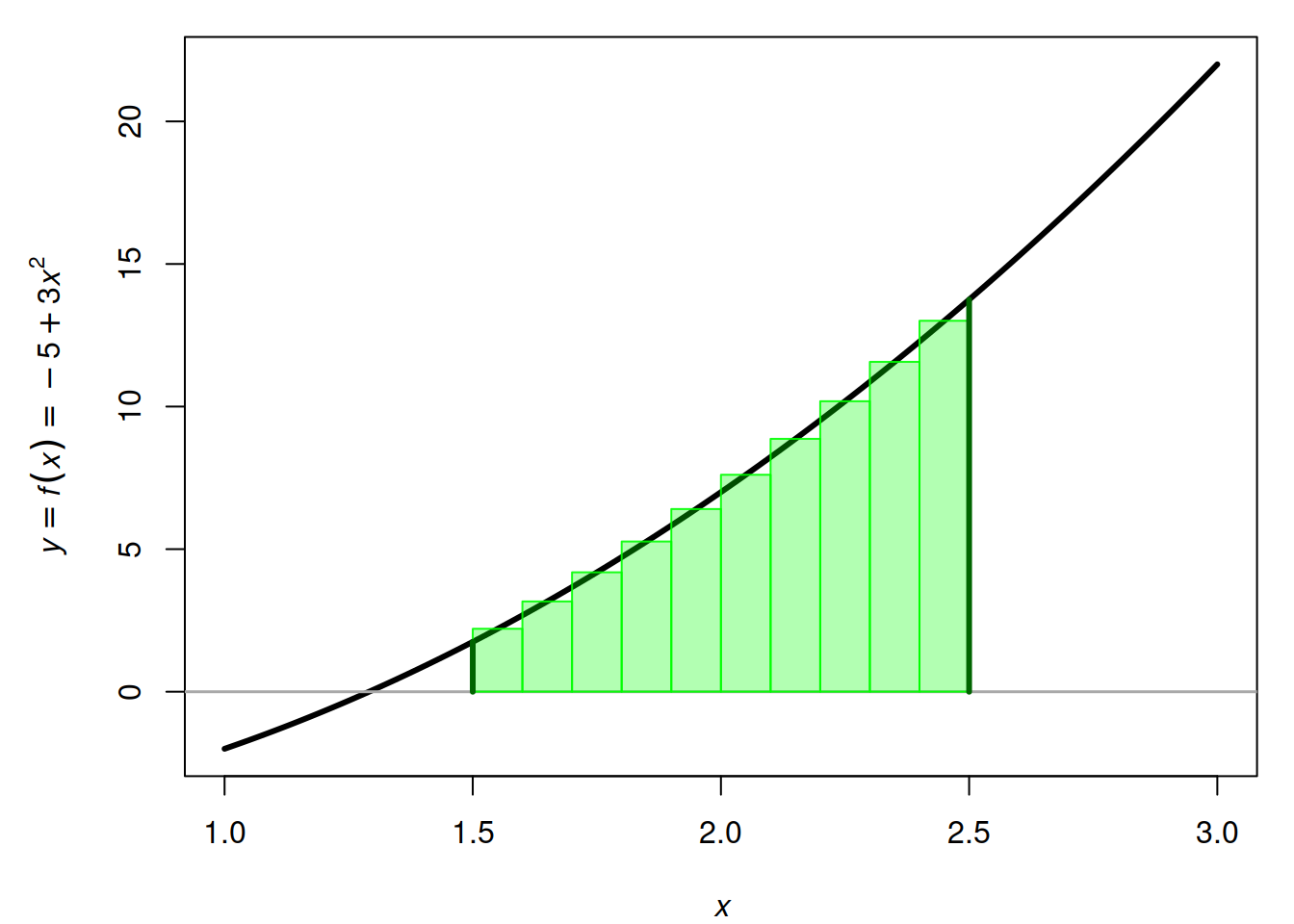
Рис. 3.6: Знаходження визначеного інтеграла як Рейманівську суму функції \(f(x) = -5 + 3x^2\).

Якщо, наприклад, шукати площу під кривою як на Рис. 3.6 поділом інтервалу між \(a = 1.5\), \(b = 2.5\) на \(10\) прямокутників (хоча їх може бути скільки завгодно), то це нескладно обчислити за допомогою R:

f <- function(x) -5 + 3*x^2
sum(sapply(seq(1.5, 2.4, 0.1)+0.05, function(x) 0.1*f(x)))

## [1] 7.2475

Із прикладу на Рис. 3.5 ми знаємо, що функція \(f(x) = -5 + 3x^2\) є першою похідною функції \(F(x) = -5x + x^3\), яка, за визначенням, є невизначеним інтегралом \(\int f(x)dx\). Відповідно,

\[ \begin{aligned} \int\limits_{1.5}^{2.5}-5 + 3x^2 dx = F(2.5) - F(1.5) = \left[ -5x + x^3 \right]_{1.5}^{2.5} = \\ [-5 \cdot 2.5 + 2.5^3] - [-5 \cdot 1.5 + 1.5^3] = 3.125 - (-4.125) = 7.25 \simeq 7.2475 \end{aligned} \]

Типові інтеграли мають наступні значення:

\[\int x^a dx = \frac{x^{a+1}}{a+1} + C \text{ } \forall \text{ } a \neq -1\]

\[\int x^{-1} dx = \int \frac{dx}{x} = \ln(|x|) + C\]

\[\int axdx = ax + C\]

\[\int \frac{1}{ax + b}dx = \frac{1}{a} \ln(|ax+b|) + C\]

\[\int \ln(x) dx = x \ln(x) -x + C\]

\[\int e^x dx = e^x + C\]

Інтегралам притаманні наступні властивості:

\[\int \limits_a^b c f(x) dx = c \int \limits_a^b f(x) dx\]

\[\int \limits_a^b f(x) + g(x) dx = \int \limits_a^b f(x) dx + \int \limits_a^b g(x) dx\]

\[\int \limits_a^a f(x)dx = 0\]

\[\int \limits_a^b f(x)dx = -\int \limits_b^a f(x)dx\]

\[\int \limits_a^c f(x)dx = \int \limits_a^b f(x)dx + \int \limits_b^c f(x)dx \text{ } \forall \text{ } a < b < c\]

Для інтегрування складних функцій використовують наступні техніки:

• інтегрування підстановкою

\[\int \limits_a^b f(g(x)) g'(x)dx = \int \limits_{g(a)}^{g(b)} f(u) du\]

де \(u = g(x)\), \(du = g'(x)dx\)

• інтегрування частинами

\[\int u (dv) = uv - \int v (du) \iff \int f(x)g'(x)dx = f(x)g(x) - \int f'(x) g(x) dx\]

де \(v = \int dv\).

В цілому, в екології рідко коли потрібно аналітично вирішити інтеграл чи похідну, однак, розуміння змісту цих операцій необхідне для подальшого розуміння статистичних підходів. В рідкісних випадках, коли необхідно вирішити певний інтеграл, має сенс скористатися онлайн-сервісами на кшталт integral-calculator.com або розрахувати значення визначеного інтегралу ітеративно за допомогою Рейманівської суми, як показано вище. Варто також мати на увазі, що деякі функції неможливо або дуже складно аналітично проінтегрувати.

---

13. Варто помітити, що хоча й індекс \(і\) присутній в діапазоні добутку, значення \(a\) не має індексу і залишається незмінним.↩︎

14. На рівні однієї, двох, трьох особин плюс-мінус одна особина багато чого змінює, в той час якщо є значення, скажімо, \(1234\), то плюс-мінус одна особина не вносить значної інформації; порівняйте \(\log_{10} 1 = 0\), \(\log_{10} 2 = 0.301\), \(\log_{10} 3 = 0.477\), і \(\log_{10} 1233 = 3.091\), \(\log_{10} 1234 = 3.091\), \(\log_{10} 1235 = 3.092\).↩︎