3.4 Розподіли ймовірності

3.4.1 Функції розподілу ймовірності

У прикладі із підкиданням монетки можливі два варіанти розвитку подій (іншими словами, із чого складається простір елементарних подій): аверс чи реверс. Відповідно, існує дві ймовірності, асоційовані із цими варіантами. Ці дві ймовірності утворюють розподіл ймовірності (probability distribution): певну функцію $f$ від кожного елементу $x$ простору елементарних подій ($\Omega$, який виступає в якості домену функції $f$ – в цьому підрозділі $\Omega$ позначимо як $\mathcal{X}$), яка повертає значення ймовірності. Коли уявити підкидання монетки як випадковий експеримент Бернулі, де $1$ відповідає випадінню аверсу (отже, $\mathcal{X} = \{0, 1\}$), то функцію розподілу ймовірності можна розписати як $f(x) = p^x (1-p)^{1-x}$, що легко скорочується в $f(1) = p$ і $f(0) = 1 - p$.

Покликання функцій розподілу ймовірності – це фундаментальний опис ідеальних випадкових змінних $X$ за $n \rightarrow \infty$. Очевидно, існує чимало розподілів окрім Бернулі, в яких змінні можна поділити на дискретні й континуальні. Фізичний зміст функції розподілу ймовірності дещо відрізняється в цих двох випадках.

Дискретний розподіл описує змінну, яка може набувати лише дискретних значень: наприклад, $x \in \mathcal{X}: \mathcal{X} = \{0, 1, 2, 3, \cdots\}$, й, відповідно, функція розподілу ймовірності обчислюється як ймовірність випадково повернути конкретне значення у випадковій змінній. Функції розподілу ймовірності для дискретних змінних називають функціями маси ймовірності (probability mass function, pmf). Прикладами таких змінних може виступати кількість особин, кількість подій тощо (скільки не старатись, а уявити $1.26$ людей важко - це завжди має бути $1$, $2$, або якесь інше ціле число). Відтак, pmf повертає ймовірність того, що випадкове значення із випадкової змінної $X$ дорівнюватиме певному значенню $x$: $P(X = x) = f(x)$.
Неперервний, або континуальний розподіл описує неперервні змінні (вага, зріст тощо). Особливістю таких змінних є те, що їх точність завжди не є кінечною. Наприклад, якщо пацієнт зважується і отримує результат 70 кг, то чи це значить що вага становить рівно 70,000 г? Можливо, можна взяти точніший зважувальний апарат, який покаже вагу 70,130 г. Але і цей показник неточний: що якщо справжня вага дорівнює $70131.76378 \ldots$ г? І це ми ще не враховуємо калібрування та похибку інструментів. Подібно до цього прикладу, в неперервній змінній $X$ ймовірність повернути будь-яке конкретне значення неможливо оцінити точно, адже воно наближається до нуля (яка ймовірність обрати людину із багатомільярдного населення планети, вага якої становитиме рівно 70,131.76378 г? Мабуть, що ця ймовірність нікчемна). Відповідно, для опису розподілів таких змінних має зміст описувати радше ймовірність отримати випадкове значення, що менше або дорівнює до певного значення: а отже, яка частка значень із випадкової змінної $X$ менше або дорівнює певному значенню $x$? В цих випадках функції густини ймовірності (probability density function, pdf) мають вигляд неперервних кривих, а шукані ймовірності знаходять інтегруванням (тобто шуканням площі під кривою) цих функцій: $P(X \leq x) = \int \limits_{-\infty}^x f(x) dx$.

В обох випадках для всякої випадкової змінної $X$ можна визначити функцію розподілу ймовірності як функцію кумулятивного розподілу (cumulative distribution function, cdf) $F(x) = P(X \leq x) \forall x$. Цікавою особливістю cdf є те, що її можна визначити навіть для $x \not\subset \mathcal{X}$: наприклад, для випадку із процесом Бернулі pmf може оцінити тільки ймовірність того, що $x = 0$ або $x = 1$. Яка ймовірність того, що випаде $0.7$? Доволі абсурдне питання, адже монетка не може випасти на $70\%$ аверсу і $30\%$ реверсу. Відтак, pmf неможливо визначити, однак cdf цілком можна: $P (X \leq 0.7) = 1-p$ (за віссю значення змінної $X$ кумулятивна ймовірність становитиме $0$ до моменту поки не $X = 0$; $(1-p)$ до моменту поки не $X = 1$; з того ж моменту, всяке значення $x \geq 1$ матиме ймовірність того що $X \leq x$ становитиме $(1 - p) + p = 1$) (Рис. 3.9.). Функція $F(x)$ є cmf якщо вона відповідає наступним вимогам:

$\lim \limits_{x \rightarrow - \infty} F(x) = 0$, $\lim \limits_{x \rightarrow \infty} F(x) = 1$,
приріст $F(x)$ не зменшується із $x$ (тобто для всяких $u > v$ $F(u) \geq F(v)$),
$F(x)$ є право-неперервною, тобто $\lim \limits_{h \downarrow 0} F(x + h) = F(x)$.

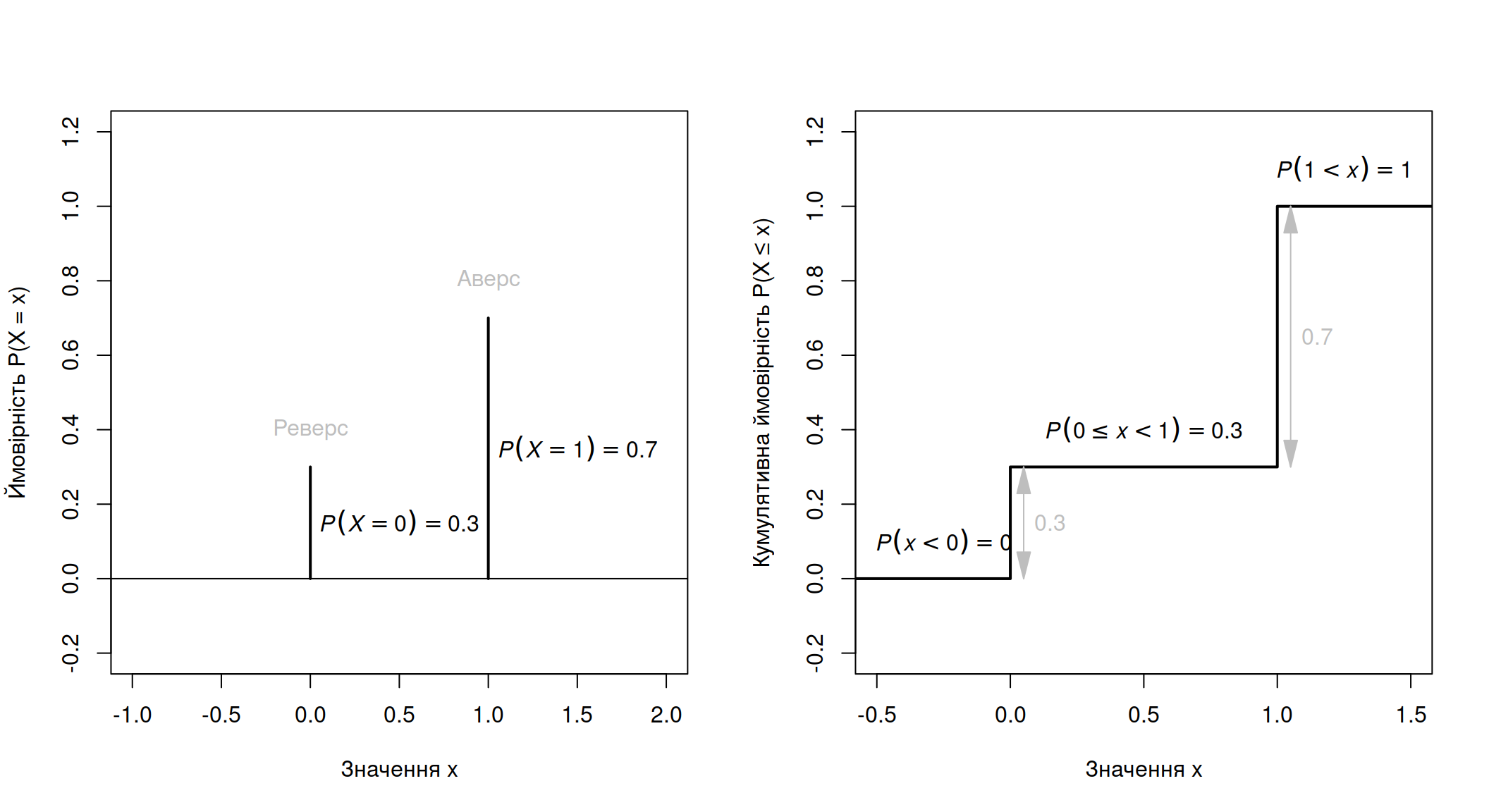
$Функція маси ймовірності і функція кумулятивного розподілу для процесу Бернулі із $p = 0.7$: елементарного підкидання монетки із $70 \%$ ймовірністю випадіння аверсу.$

Рис. 3.9: Функція маси ймовірності і функція кумулятивного розподілу для процесу Бернулі із $p = 0.7$: елементарного підкидання монетки із $70 \%$ ймовірністю випадіння аверсу.

Для дискретних змінних, pmf задана як $f(x) = P(X = x) \forall x$ і $P(X = u) = 0$ якщо $u \notin \mathcal{X}$. Для трансформації pmf в cdf можна обчислити $F(x) = P(X \leq x) = \sum \limits_{u: u \leq x} P(X = u) = \sum \limits_{u: u \leq x} f(u)$, а для протилежної трансформації cdf в pmf можна обчислити $f(x) = F(u) - \lim \limits_{h \downarrow 0} F(u - h)$. Для неперервної ж змінної, $f(u) = F(X = u) - \lim \limits_{h \downarrow 0} F(u - h) = 0$, адже $P(X = u) = 0 \forall u$; cdf можна перевести в pdf як $f(x) = \frac{d F(x)}{d x}$, і зворотньо pdf у cdf як $F(x) = \int \limits_{u: u \leq x} f(u) du$.

Важливим параметром для опису будь-якої функції розподілу ймовірності є математичне очікування, або математичне сподівання (expectation). Для всякої функції $f(x)$, математичне очікування можна знайти як середнє усіх можливих значень $x: x \in \mathcal{X}$ зважене за ймовірністю цих значень $f(x)$: відтак, для дискретних розподілів $X$ математичне очікування змінної оцінюється як $\mathbb{E}[X] = \sum \limits_{x \in \mathcal{X}} x f(x)$, а для неперервних – як $\mathbb{E}[X] = \int \limits_{x \in \mathcal{X}} x f(x) dx$. Подібно до очікування змінної, можна шукати й очікування функції змінної $g(x)$: $\mathbb{E}[g(X)] = \sum \limits_{x \in \mathcal{X}} g(x) f(x)$ або $\mathbb{E}[g(X)] = \int \limits_{x \in \mathcal{X}} g(x) f(x) dx$. Якщо очікування існує (є такі функції, для яких неможливо аналітично вирішити суми чи інтеграли), воно матиме наступні властивості:

якщо $c$ константа, то $\mathbb{E}[c] = c$,
якщо $c$ константа і $g()$ – функція, то $\mathbb{E}[c g(X)] = c \mathbb{E} [g(X)]$,
якщо $c_1$ та $c_2$ є константами і $g_1()$, $g_2()$ – функціями, то $\mathbb{E}[c_1 g_1 (X) + c_2 g_2(X)] = c_1 \mathbb{E}[g_1(X)] + c_2 \mathbb{E}[g_2(X)]$.

Математичне очікування змінної $\mathbb{E}[X]$ ще часто називають середнім (не плутати із середнім арифметичним, яке є середнім для нормального розподілу і деяких інших розподілів). Іншим важливим окремим випадком математичного очікування функції розподілу її ймовірності є її варіація $Var[X]$ – очікування середньоквадратичного відхилення випадкової змінної від її середнього:

\[ \begin{aligned} Var[X] = \mathbb{E} \left[ (X - \mathbb{E}[X])^2 \right] = \mathbb{E} \left[ X^2 - 2X \mathbb{E} [X] + (\mathbb{E} [X])^2 \right] = \\ \mathbb{E} [X^2] - 2 \mathbb{E}[X] \mathbb{E}[X] + (\mathbb{E}[X])^2 = \mathbb{E} [X^2] - 2 \mathbb{E}[X] \mathbb{E}[X] + \mathbb{E}[X] \mathbb{E}[X] = \\ \mathbb{E}[X^2] - \mathbb{E}[X] \mathbb{E}[X] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \end{aligned} \]

Функції розподілу ймовірності можуть приймати будь-який вигляд²⁰. Розгляньмо окремі випадки поширених розподілів ймовірності. В усіх випадках ми кажемо що випадкова змінна $X$ походить із певного розподілу $f(x)$ позначенням $X \sim \mathcal{A}(\theta, \cdots)$ де $\theta$ є параметром розподілу $\mathcal{A}$.

Нижче наведено формули розподілів ймовірності і, якщо доцільно, кумулятивних розподілів для окремих поширених статистичних розподілів. Також наведено значення середнього та варіації цих розподілів з точки зору параметрів і наявні шляхи обчислення оцінки параметрів (позначені як $\hat{\theta}$ для параметру $\theta$) для вибірки $x_i \in X$ розміром $n$ ²¹.

3.4.1.1 Дискретні розподіли

3.4.1.1.1 Розподіл Бернулі

Розподіл Бернулі описує дискретну змінну із лише двома класами, відтак, яку можна представити як бінарну змінну: $x \in \mathcal{X}: \mathcal{X} = \{0, 1\}$. Прикладом слугує підкидання монетки.

Позначення: $X \sim \mathcal{Bernoulli}(p)$
pmf: $f(x) = P(X = x) = p^x (1-p)^{x-1}$,
cdf: $F(x) = P(X \leq x) = 0 \mathbb{I}_x(x < 0)$, $P(X \leq x) = (1 - p) \mathbb{I}_x(0 \leq x < 1)$, $P(X \leq x) = 1 \mathbb{I}_x(1 < x)$.
середнє $\mathbb{E} [X] = \frac{N+1}{2} = p$,
варіація $Var[X] = p(1 - p)$,
оцінщик $\hat{p} = \frac{1}{n} \sum \limits_{i=1}^{n}x_i$.

3.4.1.1.2 Дискретний рівномірний розподіл

Дискретний рівномірний розподіл описує ситуацію, в якій кожна із дискретних величин ($\mathcal{X} = \{1, 2, 3, \cdots, N\}$) має однакову ймовірність потрапити у вибірку. Прикладом можуть слугувати гральні кісточки.

Позначення: $X \sim \mathcal{DU}(N)$ або $X \sim \mathcal{DU}(a, b)$ де $N = b - a + 1 \text { } \forall b \geq a$,
pmf: $f(x) = P(X = x) = \frac{1}{N} \mathbb{I}_x (x \in \{0, 1, 2, 3, \cdots, N\})$,
cdf: $F(x) = P(X \leq x) = \frac{x - a + 1}{N}$,
середнє $\mathbb{E} [X] = \frac{N+1}{2} = \frac{a+b}{2}$,
варіація $Var[X] = \frac{N^2 - 1}{12}$,
оцінщик $\hat{N} = \frac{n+1}{n} \max (x_i)$.

3.4.1.1.3 Біноміальний розподіл

Проведіть $n$ незалежних випадкових експериментів Бернулі: $X \sim \mathcal{Bernoulli}(p)$. Якщо позначити $y$ як кількість успішних експериментів в $X$ із $n$ спроб, то $Y$ описуватиметься біноміальним розподілом.

Позначення: $Y \sim \mathcal{Binomial}(n, p)$,
pmf: $f(Y) = P(Y = y) = \binom{n}{y} p^y (1-p)^{n - y} \mathbb{I}_y (y \in \{0, 1, 2, \cdots, n\})$²²,
середнє $\mathbb{E} [Y] = np$ ²³,
варіація $Var[Y] = np(1-p)$,
оцінщик $\hat{p} = \frac{y}{n}$.

3.4.1.1.4 Геометричний розподіл

Уявіть повторення випадкового експерименту Бернулі із параметром $p$ до того, поки не випаде перший успіх. В такому випадку, можна розрахувати кількість безуспішних спроб $x$ до першого успіху та кількість спроб $y$ потрібних для першого успіху. Обидві змінні описуються геометричним розподілом.

pmf:

\[f(x) = P(X = x) = p(1 - p)^x \mathbb{I}_x (0, 1, 2, \cdots, \infty)\]

\[f(y) = P(Y = y) = p(1-p)^{y-1} \mathbb{I}_y (0, 1, 2, \cdots, \infty)\]

середні

\[\mathbb{E} [X] = \frac{1-p}{p}\]

\[\mathbb{E} [Y] = \frac{1}{p}\]

варіації

\[Var[X] = \frac{1-p}{p^2}\]

\[Var[Y] = \frac{1-p}{p^2}\]

оцінщик $\hat{p} = \frac{1}{x}$.

3.4.1.1.5 Негативний біноміальний розподіл

Негативний біноміальний розподіл описує $X$ як кількість невдач перед $r$-тим успіхом в серії випадкових експериментів Бернулі із параметром $p$.

Позначення: $X \sim \mathcal{NBinom} (r, p)$,
pmf: $f(x) = P(X = x) = \binom{\text{спроби}}{\text{успіхи} + x \text{ невдач}} \cdot \text{невдачі} \cdot \text{успіхи} = \binom{x + r - 1}{r-1} (1-p) ^x p^r$,
середнє $\mathbb{E} [X] = \frac{r(1-p)}{p}$,
варіація $Var[X] = \frac{r(1-p)}{p^2}$,
оцінщик $\hat{p} = \frac{r-1}{r + x - 1}$.

Примітно, що геометричний розподіл є окремим випадком негативного біноміального розподілу. Якщо $Y$ – кількість спроб для отримання $r$ успіхів, то $Y = X + r$, $P(Y = y) = \binom{y-1}{r-1} (1-p)^{y-r} p^r$. $\mathbb{E}[Y] = \mathbb{E}[X] + r$, $Var[Y] = Var[X]$.

3.4.1.1.6 Розподіл Пуасона

Мабуть, один із найменш інтуїтивно зрозумілих але найбільш поширених розподілів. Він описує кількість подій, які відбуваються протягом визначеного вікна в просторі, при тому що всі події є незалежними один від одного. Існує чимало прикладів процесів Пуасона, наприклад, кількість людей на платформі залізничної станції в момент часу чи кількість особин популяції зареєстрованих на ділянці.

Позначення: $X \sim \mathcal{Poisson}(\lambda)$
pmf: $f(x) = P(X = x) = e^{-\lambda} \frac{\lambda^x}{x!}$, де $x \in \{0, 1, 2, 3, \cdots, \infty \}$, $\lambda > 0$,
середнє $\mathbb{E} [X] = \lambda$,
варіація $Var[X] = \lambda$,
оцінщик $\hat{\lambda} = \frac{1}{n} \sum \limits_{i=1}^{n}x_i$.

Цікаво, що $Y \sim \mathcal{Binomial}(n, p)$ із не-екстремальним значенням $(np)$ та дуже значним $n$ може бути апроксимована до розподілу Пуасона із $\lambda \approx np$.

3.4.1.1.7 Гіпергеометричний розподіл

Уявіть зліченну популяцію розміром $N$ із об’єктів, що належать до різних класів, зокрема, в якій існує $K: K \leq N$ об’єктів із певною характеристикою (наприклад, особини виду, в якому ми зацікавлені, в угрупованні різних видів²⁴). Тоді можна очікувати, що вибірка розміром $n$ із цілої популяції міститиме $x$ об’єктів із шуканого класу.

Позначення: $X \sim \mathcal{HyperGeom}(N, K, n)$,
pmf: $f(x) = P(X = x) = \frac{\binom{N}{K} \binom{N-K}{n - x}}{\binom{N}{n}}$,
середнє $\mathbb{E} [X] = n \frac{K}{N}$,
оцінщик для випадків апроксимації до розподілу Пуасона де $K/N << 1, n >> 1$: $\hat{m} = \frac{N \sum \limits_i^T x_i}{Tn}$ для вибірки $x_i \in X$ розміром $T$.

3.4.1.1.8 Нуль-упереджені моделі

Доволі цікавою родиною розподілів, котрі часто застосовують в екологічних дослідженнях, є “нуль-упереджені”, або “нуль-надуті” моделі (zero-inflated models). Такі моделі описують розподіли, в котрих значна частка спостережених значень припадає на нулі. Такі розподіли можуть описувати спостережені чисельності виду у вибірці спостережень якщо, зазвичай, ми не спостерігаємо вид (відповідно, чисельність дорівнює нулю), але якщо спостерігаємо, то чисельність відповідає якомусь позитивному цілому значенню. Відтак, якщо ігнорувати всі нульові спостереження, то чисельність описуватиметься якимось симпатичним дискретним розподілом, однак, нульові спостереження не можна просто так ігнорувати.

Насправді, нуль-упереджені моделі є комбінацією двох розподілів: один генерує нулі, в той час як інший генерує позитивні дискретні значення. Найбільш поширеним розподілом в цій родині є нуль-упереджений розподіл Пуасона (zero-inflated Poisson, ZIP): нуль-генеруюча частина цього процесу визначає чи випадкове значення дорівнюватиме нулю, і якщо ні, тоді випадкове значення отримується із звичайного розподілу Пуасона (який також може генерувати нулі, але набагато менше). Відтак, ZIP матиме два параметри: (1) ймовірність того, що нуль-генеруюча функція поверне нуль ($p$), та (2) параметр розподілу Пуасона ($\lambda$). Математично, такий розподіл можна визначити як $X \sim \mathcal{ZIP}(p, \lambda)$

\[ P(X = x_i) = \begin{cases} P(X = 0) = p + (1-p)e^{-\lambda}\\ P(X = x_i) = (1 - p) \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} \text{ } \forall \text{ } x_i = \{1, 2, 3, \cdots\} \end{cases} \]

середнє $\mathbb{E} [X] = (1-p) \lambda$,
варіація $Var[X] = (1-p)\lambda \cdot (1+p \lambda)$,
оцінщики $\hat{\lambda} = \frac{s^2 + \bar{x}^2}{\bar{x}} - 1$, $\hat{p} = \frac{s^2 - \bar{x}}{s^2 + \bar{x}^2 - \bar{x}}$ де $\bar{x} = \frac{1}{n} \sum x_i$, $s^2 = \frac{1}{n - 1} \sum (x_i - \bar{x})^2$.

3.4.1.2 Континуальні розподіли

3.4.1.2.1 Рівномірний розподіл

Рівномірний розподіл описує ситуацію, коли будь-яке значення $x$ між $a$ і $b$ має рівну ймовірність: $P(a \leq X \leq b) = 1$.

Позначення: $X \sim \mathcal{U}(a, b)$,
pdf: $f(x) = \frac{1}{b-a} \mathbb{I}_x (a \leq x \leq b)$ (примітно, що функція є константою),
cdf: $F(x) = P(X \leq x) = \frac{x-a}{b-a} \text { } \forall (a \leq x \leq b)$, але $F(X) = 0 \mathbb{I}_x(x < 0)$ і $F(X) = 1 \mathbb{I}_x (1 < x)$,
середнє $\mathbb{E} [X] = \frac{a+b}{2}$,
варіація $Var[X] = \frac{(b-a)^2}{12}$,
оцінщики $\hat{a} = \min(x_i), \hat{b} = \max(x_i)$.

3.4.1.2.2 Бета-розподіл

Доволі різноманітна родина розподілів із формою функції, яка контролюється двома параметрами, $a$ і $b$. Щодо цього розподілу, мабуть, варто просто знати про його існування. Його іноді застосовують в популяційній генетиці (Balding & Nichols 1995) та Баєсівському аналізі (Jøsang 2016).

Позначення: $X \sim \mathcal{Beta}(a, b)$,
pdf: $f(x) \propto x^{a - 1} (1-x)^{b-1} \mathbb{I}_x(0 < x < 1)$, $f(x) = \frac{\Gamma (a + b)}{\Gamma (a) \Gamma (b)} x^{a - 1} (1 - x)^{b - 1}$, де $\Gamma()$ - гамма-функція $\Gamma(\alpha) = \int \limits_0^{\infty} u^{\alpha - 1} e^{-u} du$.
середнє $\mathbb{E} [X] = \frac{a}{a + b}$,
варіація $Var[X] = \frac{ab}{(a+b)^2 (a+b+1)}$.

3.4.1.2.3 Експоненційний розподіл

Експоненційний розподіл є своєрідним неперервним аналогом геометричного розподілу і описує відстань між незалежними неперервними подіями, які відбуваються із постійним темпом. Розподіл темпів смертності в природних популяціях нагадує експоненційний (Abernethy 1979).

Позначення: $X \sim \mathcal{Exp}(\lambda)$,
pdf: $f(x) = \frac{1}{\lambda} e^{-\frac{x}{\lambda}} \mathbb{I}_x (0 \leq x \leq \infty)$,
cdf: $F(x) = 1 - e^{-\frac{x}{\lambda}}$,
середнє $\mathbb{E} [X] = \lambda$,
варіація $Var[X] = \lambda^2$,
оцінщик $\hat{(\frac{1}{\lambda})} = \frac{1}{n} \sum x_i$ із упередженням, або $\hat{(\frac{1}{\lambda})} = \frac{n-2}{\sum x_i}$.

Цікавою властивістю експоненційного процесу є відсутність пам’яті: ймовірність вижити в наступний момент часу за умови виживання до цього моменту дорівнює ймовірності вижити в будь-який момент часу ($P(X > (s+t)|X > s) = P(X > t)$).

Особливим випадком експоненційного розподілу є двопараметричний зміщений експоненційний розподіл: $f(x) = \frac{1}{\lambda} e^{-\frac{x - \mu}{\lambda}} \mathbb{I}_x (\mu \leq x \leq \infty)$, для якого середнє дорівнює $\mathbb{E}[X] = \mu + \lambda$.

3.4.1.2.4 Нормальний розподіл

Мабуть, найбільш знаменитий розподіл, яким можна описати чимало змінних в біології: розміри листків рослин, зріст людей певного віку тощо. Його логіка доволі проста і каже що змінна $X$ матиме значення $x$, які концентруються навколо якогось середнього значення $\bar{x}$, і чим сильніше $x$ відрізняються від $\bar{x}$, тим менш поширеними вони будуть. Цьому розподілу варто приділити дещо більше уваги, аніж іншим.

Позначення: $X \sim \mathcal{N}(\mu, \sigma^2)$, де параметр $\mu: \{-\infty \leq \mu \leq \infty\}$ відповідає середньому значенню (а також медіані ²⁵ та моді ²⁶), а параметр $\sigma^2: \sigma > 0$ відповідає варіації в розподілі, що виражається в ширині характерної куполоподібної кривої.
pdf: $f(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{-\left[ \frac{(x - \mu)^2}{2 \sigma^2} \right]}$,
середнє $\mathbb{E} [X] = \mu$,
варіація $Var[X] = \sigma^2$.

Хорошою демонстрацією методу максимальної правдоподібності є пошук параметрів із такої вибірки $X$ що $X \sim \mathcal{N}(\mu, \sigma^2)$. Знайдемо функцію правдоподібності:

\[\mathcal{L}(X | \mu, \sigma^2) = \prod \limits_{i=1}^n f(x_i| \mu, \sigma^2) = \prod \limits_{i=1}^n \frac{1}{\sqrt{2 \pi} \sigma} e^{-\left[ \frac{(x - \mu)^2}{2 \sigma^2} \right]} = \left( \frac{1}{\sqrt{2 \pi \sigma^2}} \right)^n \exp \left[ - \frac{\sum \limits_{i=1}^n (x_i - \mu)}{2 \sigma^2} \right]\]

Оскільки бавитись з такою формулою виглядає тією ще задачею, візьмемо логарифм правдоподібності:

\[\ln \mathcal{L}(X | \mu, \sigma^2) = - \frac{n}{2} \ln{(2 \pi \sigma^2)} - \frac{\sum \limits_{i=1}^n (x_i - \mu)}{2 \sigma^2}\]

Знайдемо оцінщик $\hat{\mu}$ першим. Для цього потрібно продиференціювати попередній вираз відносно $\mu$ і прирівняти його до нуля:

\[\frac{\partial \ln \mathcal{L}(X | \mu, \sigma^2)}{\partial \mu} = \frac{\sum \limits_{i=1}^n (x_i - \mu)}{\sigma^2} = 0\] Відтак, рішення

\[\sum \limits_{i=1}^n (x_i - \mu) = 0 \Rightarrow \sum \limits_{i=1}^n x_i - n \mu = 0 \Rightarrow \hat{\mu} = \frac{\sum \limits_{i=1}^n x_i}{n}\] Що ніщо інше як середнє арифметичне. Щодо іншого параметру, $\sigma^2$,

\[\frac{\partial \ln \mathcal{L}(X | \mu, \sigma^2)}{\partial \sigma^2} = - \frac{n}{2} \cdot \frac{2 \pi}{2 \pi \sigma^2} + \frac{\sum \limits_{i=1}^n (x_i - \mu)^2}{2 (\sigma^2)^2} = 0 \Rightarrow -n \sigma^2 + \sum \limits_{i=1}^n (x_i - \mu)^2 = 0\]

Можна підставити $\hat{\mu} = \frac{1}{n} \sum \limits_{i=1}^n x_i = \bar{x}$ і отримати

\[\hat{\sigma^2} = \frac{1}{n} \sum \limits_{i=1}^n (x_i - \bar{x})^2\]

Якщо читач дещо обізнаний в базовій статистиці, то можна помітити що цією формулою не користуються для оцінки дисперсії у вибірках із нормального розподілу. Все через те, що такий оцінщик не проходить перевірку на упередженість (bias: оцінщик вважається неупередженим якщо $\mathbb{E}[\hat{\theta}] = \theta$): якщо переформулювати (подано без покрокових обчислень, можна перевірити якщо пам’ятати що $\frac{1}{n} \sum \limits_{i=1}^n x_i \equiv \bar{x}$)

\[\hat{\sigma^2} = \frac{1}{n} \sum \limits_{i=1}^n (x_i - \bar{x})^2 = \frac{1}{n} \sum \limits_{i=1}^n x_i^2 - (\bar{x})^2\]

Тоді (пам’ятаючи що $\sigma^2 = Var[X] = \mathbb{E} [X^2] - (\mathbb{E} [X])^2 = \mathbb{E} [X^2] - \mu^2$)

\[ \begin{aligned} \mathbb{E} [\hat{\sigma^2}] = \mathbb{E} \left[ \frac{1}{n} \sum \limits_{i=1}^n x_i^2 - (\bar{x})^2 \right] = \frac{1}{n} \sum \limits_{i = 1}^n \mathbb{E} [x_i^2] - \mathbb{E} [\bar{x}^2] = \\ \frac{1}{n} \sum \limits_{i = 1}^n (\sigma^2 + \mu^2) - (\frac{\sigma^2}{n} + \mu^2) = (1 - \frac{1}{n}) \sigma^2 \neq \sigma^2 \end{aligned} \]

Натомість, неупередженим оцінщиком $\hat{\sigma^2}$ є щось, що називають дисперсією вибірки: $\hat{\sigma^2} = s^2 = \frac{1}{n-1} \sum \limits_{i=1}^n (x_i - \bar{x})^2$. Аби уникнути термінологічної плутанини (а вона чомусь завжди наявна в оцінках варіації), варто визначити наступні дескриптори варіації, що часто застосовуються до вибірок із нормальним розподілом (використовуйте тест Шапіро-Вілка (Shapiro-Wilk test) для перевірки нормальності вибірки; $p > 0.05$, на відміну від більшості статистичних тестів, є підставою вважати вибірку нормально розподіленою):

дисперсія (sample variance) є неупередженим оцінщиком параметру $\sigma^2$ нормального розподілу у вибірці: $s^2 = \frac{1}{n-1} \sum \limits_{i=1}^n (x_i - \bar{x})^2$, якому в R відповідає функція var(),
середньоквадратичне відхилення описує варіацію вибірки незалежно від її розподілу: $v^2 = \frac{1}{n} \sum \limits_{i=1}^n (x_i - \bar{x})^2$; однак набагато частіше під цим терміном (як і будемо ми) розуміють кориговане стандартне відхилення (standard deviation, SD): $s = \sqrt{\frac{1}{n-1} \sum \limits_{i=1}^n (x_i - \bar{x})^2}$, якому в R відповідає функція sd(),
стандартна помилка (standard error, SE) описує відхилення вибіркового середнього $\bar{x}$: $\frac{s}{\sqrt{n}}$,
коефіцієнт варіації (coefficient of variation, CV) нормалізує стандартне відхилення на середнє арифметичне і часто позначається у відсотках: $CV = 100 \% \cdot {s}/{\hat{\mu}}$.

Щодо важливості нормального розподілу в статистиці, варто згадати закон великих чисел та центральну граничну теорему. Закон великих чисел стверджує, що якщо із генеральної сукупності ²⁷ незалежно і багаторазово набирати окремі вибірки, то усереднена статистика²⁸ цих вибірок наближається до істинного значення статистики генеральної сукупності, якщо таке існує. В контексті нормального розподілу, середні вибірок ($\hat{\mu}$) з генеральної сукупності конвергують до середнього генеральної сукупності $\mu$. Центральна гранична теорема ж постулює, що в множині таких незалежних змінних $X_1, X_2, X_3, \cdots, X_n$, що $\mathbb{E} [X_i] = \mu$, $Var[X_i] = \sigma^2$, незалежно від розподілу окремих змінних $X_i$, за $n \rightarrow \infty$ розподіл змінних $\sqrt{n} (\frac{1}{n}\sum \limits_{i=1}^n X_i - \mu)$ конвергує до $\mathcal{N}(0, \sigma^2)$. Іншими словами, яким би не був розподіл генеральної сукупності, розподіл середніх значень вибірок із такої генеральної сукупності буде нагадувати нормальний розподіл.

Корисною технікою є z-стандартизація (z-scaling), за допомогою якої будь-яку вибірку можна трансформувати в таку, в якої $\mu = 0, \sigma^2 = 1$ (припускаючи, що вибірка розподілена нормально, але техніка працює для будь-якого розподілу): $z_i = \frac{x_i - \bar{x}}{s}$. Такий нормальний розподіл, що $\mathcal{N} (\mu = 0, \sigma^2 = 1)$ називається cтандартним нормальним розподілом.

3.4.1.2.5 Лог-нормальний розподіл

Змінна $X$ розподілена лог-нормально ($X \sim L\mathcal{N}(\mu, \sigma^2)$) якщо $\ln(X) \sim \mathcal{N}(\mu, \sigma^2)$. Відтак, якщо поглянути з іншого боку, то якщо $Y \sim \mathcal{N}(\mu, \sigma^2)$, то $X = e^Y \sim L\mathcal{N}(\mu, \sigma^2)$.

Середнє $\mathbb{E} [\ln (X)] = \mu, \mathbb{E}[X] = e^{\mu + \frac{\sigma^2}{2}}$,
варіація $Var[\ln(X)] = \sigma^2, Var[X] = \exp [2(\mu - \sigma^2)] - \exp [2 \mu + \sigma^2]$.

3.4.1.2.6 Розподіл Коші

Доволі дивний розподіл, який формою нагадує нормальний із набагато гострішим піком та товстішими хвостами.

Позначення: $X \sim \mathcal{Cauchy}(x_0, \gamma)$, де $\gamma$ регулює форму кривої, а $x_0$ відповідає локації піку.
pdf: $f(x) = \frac{1}{\pi} \left[ \frac{\gamma}{(x - x_0)^2 + \gamma^2} \right]$

Дивність цього розподілу полягає в тому, що його середнє й варіація неможливо аналітично визначити. Оцінки середнього арифметичного і cередньоквадратичного відхилення не конвергують зі збільшенням розміру вибірки, а єдиним більш-менш точним методом оцінки параметру форми $\hat{\gamma}$ є медіана абсолютних значень вибірки.

3.4.2 Опис розподілу змінної (описова статистика)

Уявімо вибірку змінної $X \sim \mathcal{N}(\mu = 15, \sigma^2 = 9)$ розміром $n = 1000$:

# визначимо рандомне зерно для повторюваності коду
set.seed(1234)

# визначимо змінну як випадкову вибірку із нормального розподілу із визначеними параметрами
X <- rnorm(n = 1000, mean = 15, sd = sqrt(9))

Як описати тенденції цієї вибірки одним-двома параметрами? Мабуть, більшість автоматично скажуть “давайте порахуємо середнє”, хтось додасть “і варіацію у вигляді середньоквадратичного відхилення чи дисперсії”. Натомість, навіть на цьому етапі вирішення статистики для опису змінної варто задати собі питання: а що нам ці статистики дадуть? По-перше, як мінімум, ми хочемо отримати такі значимі і продумані статистики, із якими, якщо потрібно, можна спробувати відтворити вибірку. По-друге, як ми побачили в попередньому підрозділі, існує чимало розподілів ймовірності, і найгірше, що можна зробити – це спробувати описати змінну із певним розподілом параметром не цього розподілу (наприклад, намагатись оцінити параметри $a$ і $b$ бета-розподілу, коли вибірка відповідає Пуасонівському процесу). Дуже важливим неписаним правилом статистичного аналізу є те, що в більшості випадків оцінщик чи статистичний тест видасть якийсь результат для даних, які в нього введені, і, може, навіть видасть якесь значення $p$ (див. нижче), але цей результат нічого не значить якщо обрано некоректну статистичну процедуру для певного набору даних. Крім того, завжди мати на увазі принцип “garbage in, garbage out” (“сміття на вході, сміття на виході”): навіть якщо логіка статистичного аналізу правильна і програма функціонує коректно, результати не можна вважати валідними якщо вхідні дані помилкові.

Це дуже довгий спосіб сказати, що для вибору метрики центральної тенденції у вибірці варто враховувати розподіл цієї вибірки. Не можна розраховувати, скажімо, середнє арифметичне просто тому, що так зручно. Натомість, вибір статистики повинен бути виважений і відповідати передбаченому розподілу змінної²⁹. В нашому випадку, ми знаємо що $X$ згенеровано як нормальний процес, але давайте про всяк випадок перевіримо чи ця змінна дійсно розподілена нормально.

shapiro.test(X)

## 
##  Shapiro-Wilk normality test
## 
## data:  X
## W = 0.99737, p-value = 0.1053

Тест Шапіро-Вілка видає $p = 0.105 > 0.05$, що у випадку цього тесту дає підстави вважати, що змінна дійсно розподілена нормально. Відтак, центральну тенденцію можна описати середнім арифметичним, адже воно відповідає оцінщику очікування нормального розподілу.

mean(X)

## [1] 14.92021

Які є альтернативи середньому арифметичному? Популярним вибором є медіана, особливо в якості непараметричної статистики – такої статистики, яка вимагає мінімальних передбачень щодо розподілу даних і може бути використана для змінних із будь-яким розподілом. В багатьох випадках змінні в даних матимуть дивний (асиметричний, бімодальний тощо) розподіл. В таких випадках можна спробувати провести тест Шапіро-Вілка, який скоріш за все не підтримає припущення про нормальний розподіл ($p < 0.05$). Якщо є припущення про якийсь інший розподіл, його можна перевірити із тестом Колмогорова-Смірнова³⁰. Порівняймо нашу вибірку із нормальним розподілом (хоча ми й так вже знаємо із тесту Шапіро-Вілка відповідь).

# z-стандартизація вибірки потрібна, адже розподіл для порівняння є за замовчуванням стандартним нормальним розподілом
Z <- scale(X)

# порівняймо із ідеальним випадком, для чого наведемо назву функції кумулятивного нормального розподілу
ks.test(x = Z, y = "pnorm")

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  Z
## D = 0.021443, p-value = 0.7474
## alternative hypothesis: two-sided

# альтернативно, можна для порівняння використати іншу випадкову вибірку із нормальним розподілом
ks.test(Z, rnorm(n = length(Z)))

## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  Z and rnorm(n = length(Z))
## D = 0.026, p-value = 0.8879
## alternative hypothesis: two-sided

# або порівняти вихідну не-стандартизовану змінну із випадковою нормальною вибіркою із середнім та варіацією вихідної вибірки
ks.test(X, rnorm(n = length(X), mean = mean(X), sd = sd(X)))

## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  X and rnorm(n = length(X), mean = mean(X), sd = sd(X))
## D = 0.036, p-value = 0.5361
## alternative hypothesis: two-sided

Оскільки вибірка $X \sim \mathcal{N}()$, можна перебачити що медіана приблизно дорівнюватиме середньому арифметичному, відтак, для нормальних вибірок немає змісту наводити інший параметр окрім середнього.

mean(X)

## [1] 14.92021

median(X)

## [1] 14.88062

Якби ми підходили до непараметричного аналізу вибірки із не-нормальним розподілом, варто було би використовувати лише медіану. Класичним прикладом є уявний експеримент із вибіркою з трьох людей: одним мільйонером (зарплатня $\$1000000$ на місяць) та двома бідняками ($\$100$ на місяць). Яка середня зарплатня і яка медіана в такій популяції?

mean(c(1000000, 100, 100))

## [1] 333400

median(c(1000000, 100, 100))

## [1] 100

Очевидно, середнє значення $\$330400$ нічого не значить в цій значно асиметричній вибірці, адже біднякам така “середня температура по лікарні” аж ніяк не допомагає. Медіана ж є набагато більш репрезентативною статистикою.

Скажімо, ми хочемо описати розподіл змінної, але не маємо змоги надати значення кожного значення в змінній (особливо якщо йдеться про значний розмір вибірки). Навіть у випадку нормально розподіленої змінної середнього значення недостатньо, адже воно не надає жодної ідеї про розмах кривої, тобто її варіацію. Як тоді читач може відтворити вашу змінну? Хорошою ідеєю є надати значення оцінщика варіації. Наприклад, сказати що $X \sim \mathcal{N}(\mu = 15, \sigma^2 = 9), n = 1000$ цілком достатньо аби відтворити змінну за допомогою комп’ютера, наприклад, в R як rnorm(n = 1000, mean = 15, sd = sqrt(9)).

У випадку невідомого розподілу змінної, можна використати перцентилі – значення у вибірці, які розділяють цю сортовану вибірку на визначені частки. Наприклад, якщо ми позначимо $\alpha$-тий перцентиль змінної $X$ як $x_{\alpha}$, тоді $P(X \leq x_{\alpha}) = \alpha$ (тобто у вибірці $X$ $99\%$ значень $x_i$ будуть меншими або дорівнюватимуть значенню $x_{\alpha = 0.99}$). В якості непараметричного опису розподілу можна як мінімум подати перцентилі для $\alpha = 0.025$ і $\alpha = 0.975$ – тоді $95\%$ змінної перебуватимуть в межах цих двох значень. Для більш детального опису розподілу можна подати й інші межі: $60 \%$ ($\alpha = \{0.2, 0.8\}$), $80 \%$ ($\alpha = \{0.1, 0.9\}$) тощо. Медіана відповідає $\alpha = 0.5$, тобто рівно половина значень у вибірці буде менша за медіану, рівно половина – більша.

Якщо є вибірка із дивним розподілом і його не вдається описати жодним із перелічених вище параметричним розподілом, корисною технікою є ядрова оцінка густини розподілу (kernel density estimation, KDE,). Існує декілька його варіацій, але в найпростішому вигляді процедура наступна: (1) для кожного спостереження $x_i$ побудуймо елементарний нормальний розподіл із фіксованою варіацією $\sigma^2 = a$ такий що $\mathcal{N}_i = \mathcal{N}(\mu = x_i, \sigma^2 = a)$, і (2) додаймо всі такі розподіли $\mathcal{N}_i$ в один. Якщо суму цих функцій стандартизувати таким чином, щоб її інтеграл дорівнював одиниці, на виході отримаємо валідну функції густини ймовірності, яка точно описує розподіл вихідної змінної. На практиці функція (kernel function) із кроку (1) складніша за простий нормальний розподіл, що дозволяє змінювати розмір вікна, в межах якої ця функція враховує точки спостережень, котрі впливають на розмір ядра – так званий параметр пропускної здатності (bandwidth) що може змінювати “чіткість” результуючої функції.

На жаль, мало хто приділяє увагу таким деталям і обмежується значеннями середнього і якогось оцінщика варіації на кшталт “$\bar{x} = 14.920 \pm 2.992 SD$” чи “$\bar{x} = 14.920 \pm 0.095 SE$”. В принципі, середнього і показника похибки достатньо для висновку щодо форми розподілу змінної (знову ж, якщо відомо що ця змінна розподілена нормально). Головним застереженням тут є те, що необхідно завжди зазначати використану статистику похибку. Крім стандартного відхилення (SD) та стандартної похибки (SE) таким можуть також слугувати довірчі інтервали (confidence interval). Довірчий інтервал статистики оцінює, в якому інтервалі лежатимуть значення статистики за багаторазового повтору експерименту із певним рівнем довіри $\gamma$ (зазвичай, $\gamma = 0.95$, у випадку чого інтервал зветься “95% довірчим інтервалом”, “95% CI”). Цей інтервал не означає, що точність оцінки становить плюс-мінус якесь значення, особливо коли вибірка асиметрична (відтак, інтервал необхідно позначати власне як інтервал без використання знаку плюс-мінус). Натомість, ми можемо очікувати що за багаторазового незалежного повторення експерименту значення статистики лежатиме в межах довірчих інтервалів у $100 \cdot \gamma \%$ випадків.

В переважній більшості випадків оцінка довірчих інтервалів є параметричною процедурою, унікальною для окремої статистики і окремого розподілу. Поширеною помилкою є, наприклад, оцінка довірчих інтервалів середнього арифметичного нормального розподілу для частки (якогось значення між $0$ і $1$): така оцінка передбачатиме, наприклад, існування значень частки $<0$ і $>1$, що є абсурдом. В разі, якщо не вдається знайти адекватний оцінщик статистики в певному розподілі, адекватним варіантом може бути пермутаційна оцінка інтервалу як перцентилів ($2.5\%, 97.5\%$) розподілу статистики згенерованої пермутаціями.

Вибір оцінки похибки видається залежним від моди в певних сферах, і, насправді, кожен із них має право на існування допоки дослідник чітко позначає, яка саме похибка використана. Найчастіше про це забувають в графіках змінних, що є доволі трагічним: від вибору метрики “розмаху” залежить весь умовивід із графіку. Нижче (Рис. 3.10. – код також додано, раптом комусь знадобиться) наведено потенційні візуальні відображення розподілу в одній однієї й тієї ж вибірки $X$.

Xdf <- tibble(X = X)

f_3_10_a <- Xdf %>% 
  ggplot(aes(x = 0, y = X)) +
  geom_jitter() +
  xlab("") + ylab("Значення X") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

f_3_10_b <- Xdf %>% 
  ggplot(aes(x = X)) +
  geom_bar() +
  scale_x_binned() +
  xlab("Значення X") + ylab("Частота")

f_3_10_c <- Xdf %>% 
  ggplot(aes(x = X)) +
  geom_density(fill = "gray") +
  xlab("Значення X") + ylab("Частота")

f_3_10_d <- Xdf %>% 
  ggplot(aes(x = 0, y = X)) +
  geom_violin(fill = "gray") +
  ylim(4, 25) +
  xlab("") + ylab("Значення X") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

f_3_10_e <- Xdf %>% 
  ggplot(aes(x = 0, y = X)) +
  geom_boxplot() +
  ylim(4, 25) +
  xlab("") + ylab("Значення X") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

X_sum <- Xdf %>%
  summarise(n = n(), mu = mean(X), sd = sd(X), se = sd/sqrt(n))

f_3_10_f <- X_sum %>% 
  ggplot(aes(x = 0, y = mu)) + 
  geom_point(aes(x = 0, y = mu)) +
  geom_errorbar(aes(x = 0, ymin = mu - sd, ymax = mu + sd), 
                width = 0.4) +
  ylim(4, 25) +
  xlab("") + ylab("Середнє X ± SD") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

quantiles_95 <- function(x) {
  r <- quantile(x, probs=c(0.05, 0.25, 0.5, 0.75, 0.95))
  names(r) <- c("ymin", "lower", "middle", "upper", "ymax")
  r
}

f_3_10_g <- ggplot(Xdf, aes(x = 0, y = X)) +
    guides(fill = F) +
    stat_summary(fun.data = quantiles_95, geom = "boxplot") +
  ylim(4, 25) +
  xlab("") + ylab("Медіана ± 50%, 95% CI") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

f_3_10_h <- X_sum %>% 
  ggplot(aes(x = 0, y = mu)) + 
  geom_point(aes(x = 0, y = mu)) +
  geom_errorbar(aes(x = 0, ymin = mu - se, ymax = mu + se), 
                width = 0.4) +
  xlab("") + ylab("Середнє X ± SE") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

f_3_10_i <- X_sum %>% 
  ggplot(aes(x = 0, y = mu)) + 
  geom_col(position = position_dodge()) +
  geom_point(aes(x = 0, y = mu)) +
  geom_errorbar(aes(x = 0, ymin = mu - se, ymax = mu + se), 
                width = 0.4) +
  xlab("") + ylab("Значення X ± SE") +
  theme(axis.ticks.x = element_blank(),
        axis.text.x = element_blank())

ggarrange(plotlist = list(
  f_3_10_a, f_3_10_b, f_3_10_c, f_3_10_d, f_3_10_e, f_3_10_f, f_3_10_g, f_3_10_h, f_3_10_i
), labels = letters[1:9])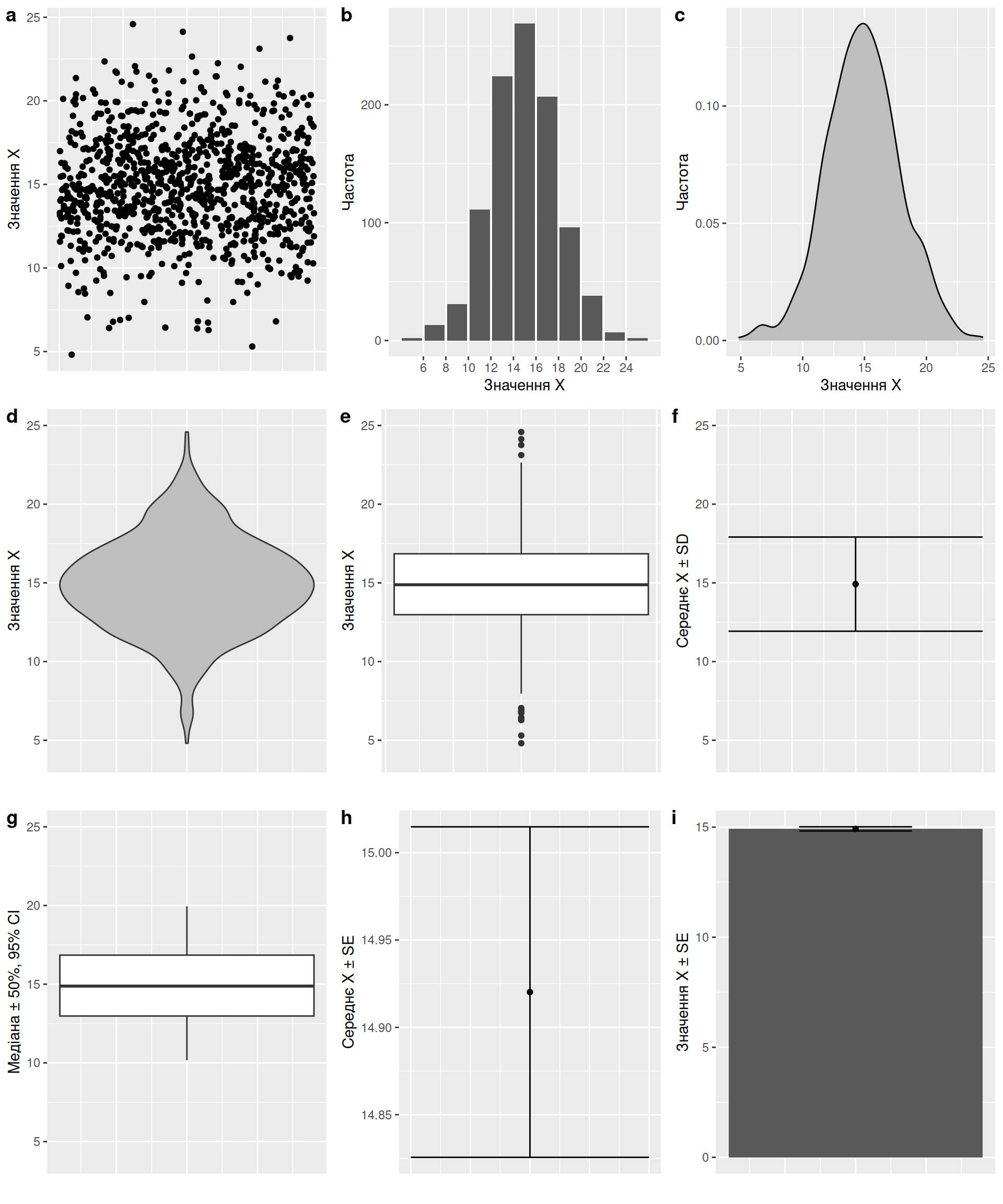

Різноманітні способи зобразити розподіл змінної: **(a)** хмара точок спостережень - найкращий спосіб зобразити сирі даних, якщо точок відносно небагато; **(b)** гістограма - колонки відповідають рівномірним діапазонам значень; **(c)** ядрова оцінка густини розподілу, своєрідна неперевна гістограма, що є кращою альтернативою гістограмі у випадку континуальних змінних; **(d)** 'скрипко-графік' (violin plot) є дзеркальним відображенням ядрової оцінки розподілу; **(e)** класичний 'коробко-графік' (boxplot) де жирна центральна лінія відповідає медіані, межі коробки - міжквартильному розмаху (між 25- та 75-тими перцентилями), межі вусів - розмаху даних без 'викидів', а окремі точки - власне викидам (спостереження, що потрапили за межі 1.5 міжквартильного розмаху від 25- чи 75-ого перцентилю); **(f)** відображення середнього арифметичного і відхилення у формі стандартного відхилення; **(g)** 2.5-, 25-, 50-, 75-, та 97.5-ті перцентилі, які можуть сприйматися як довірчі інтервали розподілу (але не його середнього); **(h)** відображення середнього арифметичного і відхилення у формі стандартної помилки - зверніть увагу на шкалу, розмах вусів набагато менший за інші за рахунок значного розміру вибірки; **(i)** відверто найгірший варіант - 'динаміто-графік' (dynamite plot), який малює колонку чогось (на відміну від гістограми, ця колонка рідко має будь-який зміст, наприклад, у вибірці нема значень нижче за 4, але зона від 0 до середнього все одно замальована) із 'вусами' стандартної помилки.

Рис. 3.10: Різноманітні способи зобразити розподіл змінної: (a) хмара точок спостережень - найкращий спосіб зобразити сирі даних, якщо точок відносно небагато; (b) гістограма - колонки відповідають рівномірним діапазонам значень; (c) ядрова оцінка густини розподілу, своєрідна неперевна гістограма, що є кращою альтернативою гістограмі у випадку континуальних змінних; (d) ‘скрипко-графік’ (violin plot) є дзеркальним відображенням ядрової оцінки розподілу; (e) класичний ‘коробко-графік’ (boxplot) де жирна центральна лінія відповідає медіані, межі коробки - міжквартильному розмаху (між 25- та 75-тими перцентилями), межі вусів - розмаху даних без ‘викидів’, а окремі точки - власне викидам (спостереження, що потрапили за межі 1.5 міжквартильного розмаху від 25- чи 75-ого перцентилю); (f) відображення середнього арифметичного і відхилення у формі стандартного відхилення; (g) 2.5-, 25-, 50-, 75-, та 97.5-ті перцентилі, які можуть сприйматися як довірчі інтервали розподілу (але не його середнього); (h) відображення середнього арифметичного і відхилення у формі стандартної помилки - зверніть увагу на шкалу, розмах вусів набагато менший за інші за рахунок значного розміру вибірки; (i) відверто найгірший варіант - ‘динаміто-графік’ (dynamite plot), який малює колонку чогось (на відміну від гістограми, ця колонка рідко має будь-який зміст, наприклад, у вибірці нема значень нижче за 4, але зона від 0 до середнього все одно замальована) із ‘вусами’ стандартної помилки.

Зображення розподілу вибірок часто необхідно для порівняння двох (чи більше) вибірок. Наприклад, уявіть вибірки $A$ і $B$, які відповідають промірам певного параметру (наприклад, маси тіла) в двох групах (скажімо, субпопуляціях виду). Залежно від того, чому відповідають вуса графіків, висновок із їх візуального зображення відрізнятиметься:

якщо вуса SD двох вибірок перекриваються між собою, це не може бути достатнім доказом статистичної відмінності між вибірками (необхідні додаткові тести, наприклад, t-тест Ст’юдента або непараметричний аналог);
якщо вуса SE перекриваються і дві вибірки мають однакові розміри, статистичної відмінності між вибірками, скоріш за все, немає; якщо вуса не перекриваються, необхідне додаткове тестування;
якщо вуса 95% CI перекриваються, необхідне додаткове тестування; якщо ж вони не перекриваються, скоріш за все, існує істотна різниця між вибірками.

Загалом, графічне зображення розмаху вибірок викликає чимало плутанини із висновками (Payton et al. 2003, Belia et al. 2005, Cumming et al. 2007). Порадою слугуватиме завжди зазначати які саме метрики розмаху зображені й проводити додаткове статистичне тестування гіпотез.

…особливо pdf: часто значення функції перевищує одиницю, що викликає справедливе питання “а як ймовірність може бути більша за одиницю?”. Не може, але й ця функція не повертає ймовірність. Її інтеграл повертає ймовірність.↩︎
Варто зауважити, що формули оцінщиків взяті із відкритих джерел, включно із постами блогів. Кожен розподіл має своєрідну ситуацію із оцінщиками, і виведення оцінщиків не завжди проводиться методом максимальної правдоподібності чи за допомогою момент-генеруючих функцій (ми не торкаємось цього методу), ба того, такі оцінщики іноді є упередженими (biased). Використовувати оцінщики параметрів необхідно із застереженнями!↩︎
…cdf біноміального розподілу існує, але його складно вивести і він все одно мало що скаже; варіацію біноміального розподілу також шукати відносно непросто.↩︎
Обчислення очікування із біноміальними коефіцієнтами включає розкладання біному: $(a + b)^n = \sum \limits_{x = 0}^n \binom{n}{x} a^x b^{n - x}$.↩︎
Застосування гіпергеометричного розподілу в реальних задачах екології угруповань може бути складним, адже чисельності видів можуть сягати сотень і тисяч, й обчислення біноміальних коефіцієнтів видасть дуже великі числа – іноді настільки великі, що комп’ютер не може їх обчислити і зве безкінечністю. Аби обійти обмеження стандартної комп’ютерної архітектури в нагоді можуть стати функції із бібліотеки gmp для R.↩︎
Медіана – значення в сортованій послідовності випадкової змінної $X$, яке розділяє цю послідовність на дві частини однакового розміру; медіана тісно пов’язана із поняттями перцентилів $x_{\alpha}$ – такими значеннями $x$, які більше за частку $\alpha$ випадкової змінної $X$ (наприклад, перцентиль $x_{\alpha = 0.95}$ – це таке значення, що в змінній $X$ $95 \%$ значень менше або дорівнюють $x_{\alpha = 0.95}$). Медіана відповідає перцентилю із $\alpha = 0.5$.↩︎
Мода – найбільш поширене значення у вибірці.↩︎
Генеральна сукупність – поширене поняття в статистиці; якщо спостерігач обрав вибірку значень (наприклад, вага особин модельного виду), ця вибірка є лише обмеженою підмножиною генеральної сукупності, розмір якої апроксимує до безкінечності. Ми припускаємо що вибірка є репрезентативною щодо генеральної сукупності, отже, розподіл ймовірності в генеральній сукупності апроксимує до розподілу в генеральній сукупності. Неможливо набрати вибірку розміром із розмір генеральної сукупності – спостерігач завжди пропустить бодай один зразок.↩︎
Статистика – інше слово для параметру вибірки або параметру тесту. Середнє арифметичне є статистикою, дисперсія є статистикою тощо.↩︎
Наприклад, як розрахувати узагальнену кількість особин виду для повторних спостережень на певній локації? Свого часу мені казали рахувати максимальну кількість особин між спостереженнями, однак такий підхід не є коректним. Натомість, якщо розглядати спостереження особин як біноміальний процес або процес Пуасона, за обох розподілів середнє арифметичене слугує виправданим оцінщиком. Для поглибленого погляду в цю тему, див. ймовірність детекції.↩︎
Тест Колмогорова-Смірнова використовують для перевірки гіпотези, що дві вибірки отримані із одного неперервного розподілу. Іншими словами, тестом Колмогорова-Смірнова можна перевірити розподіл змінної (навіть непараметричний розподіл, якщо наявна його адекватна pdf).↩︎