4.6 Динаміка та стабільність

Якщо ви колись зайшли ввечері на кухню, ввімкнули світло, і тим налякали самотнього таргана на підлозі, то ви, мабуть, знаєте – це тільки початок. Якщо ви не почнете прибирати всі рештки їжі, закривати смітник, розкладати отруту, то у вас дуже хороші шанси з часом почати помічати все більше й більше тарганів. Вітаю, на вашій кухні тепер існує ваша власна популяція! Всяке життя намагається розмножуватись, і таргани – не виняток. Достатньо однієї заплідненої самиці прусака рудого (Blatella germanica) аби відкласти оотеку—пакет із декількома десятками яєць,—і вже за два місяці ви матимете із десяток статевозрілих самиць (Рис. 4.2) (Fan et al. 2022). Якщо на всіх вистачить їжі й виживання особин нічим не пригнічене, всі ці самиці так само відкладуть свої оотеки, і лише за чотири місяці від колонізації вашої кухні ви дивитесь на популяцію розміром зо п’ять сотень особин, за шість місяців – із шість тисяч особин, і так далі⁵².

В цьому прикладі немає нічого особливого щодо тарганів, адже всі організми розмножуються. Звісно, в різних видів – різні стратегії щодо розміру потомства, частоти розмноження, особливостей статевого чи безстатевого розмноження тощо, однак, в цілому, популяція будь-якого виду збільшується із часом за сприятливих умов. Звісно, умови не завжди є сприятливими: в природі завжди виявляється, що існує смертність особин з різних причин (хижаки, патогени, старість), репродуктивний потенціал особин залежить від різних факторів (наприклад, віку), абіотичні фактори можуть виявитись несприятливими для розмноження (як би таргани на старалися, але якщо температура середовища нижча за 0°С, то вони замерзнуть задовго до того як встигнуть розмножитись), ресурси є завжди обмеженими, і, врешті, існує імміграція особин в популяцію та еміграція із популяції.

В найпростішому вигляді ми можемо уявити чисельність популяції $N$ в будь-який момент часу $\tau$ як продукт чисельності популяції в попередній момент часу ($\tau-1$). Від популяції в минулий момент часу варто відняти всі особини, які померли ($D$) чи емігрували із популяції ($E$) та додати особини, котрі народились ($B$) та іммігрували в популяцію ($I$):

\[N_{\tau} = N_{\tau - 1} - D - E + B + I\]

Іншими словами, розмір популяції сьогодні дорівнює розміру популяції вчора мінус смертність й еміграція та плюс народжуваність й імміграція. Оскільки крок часу не завжди відповідає дню, а може відповідати й іншим одиницям часу, а час сам по собі є континуальною змінною, це рівняння можна переписати у вигляді різницевого рівняння (дискретного брата диференційного рівняння):

\[\frac{\Delta N_t}{\Delta \tau} = \frac{-D-E+B+I}{\Delta \tau}\]

Це рівняння варто читати як “зміна значення $N$ за зміни часу на один крок”. І ось у вас є базовий математичний опис динаміки будь-якої популяції в часі. Звісно, це рівняння нічого не каже про інші фактори, перелічені вище – до цього ми дійдемо пізніше. Наразі, для спрощення, нам потрібно забути про еміграцію й імміграцію в нашій моделі ($E=0$, $I=0$), і уявити що популяція є закритою. Динаміку популяції відтак можна описати лише через $(-D+B)$. Ці обидві змінні описують кількість особин, так само як і $N$, а отже їх можна перевести в частки: $b$ як приріст популяції ($b = B/N$) та $d$ як смертність популяції ($d = D/N$). Комбінований ефект приросту та смертності популяції можна визначити як внутрішній темп зростання (intrinsic rate of growth, або per capita population growth rate, PGR) $r = b - d$. Якщо $r>0$, то розмір популяції зростає, в той час як $r < 0$ описує популяцію на шляху до вимирання. Якщо $r = 0$, це може означати лише що темпи смертності дорівнюють темпам народжуваності, і, відтак, чисельність популяції незмінна з часом.

4.6.1 Експоненційний ріст

Якщо прийняти початковий розмір популяції як $N_0$, то чи можна спрогнозувати розмір популяції в будь-який інший момент часу? В моделі із дискретним часом (тобто де час поділений на дискретні кроки, $\tau = 0, 1, 2, 3, \cdots$) станом на наступний крок часу, $\tau=1$, розмір популяції можна описати як $N_1 = N_0 + bN_0 - dN_0$. В принципі, це рівняння нескладно спростити:

\[N_1 = (1 + b - d)N_0\]

Оскільки $(b-d)$ є визначенням темпу зростання популяції на особину ($r=b-d$), це рівняння можна переписати як

\[N_1 = (1+r)N_0\]

За стабільного зростання популяції за кожного кроку розмір популяції збільшується у фіксованому факторі: якщо визначити темп зростання популяції як $\lambda$, цей фактор дорівнюватиме $\lambda = \frac{N_{\tau}}{N_{\tau-1}}$, а, отже, $N_\tau = \lambda N_{\tau-1}$. В поняттях попереднього рівняння,

\[N_1 = (1+r)N_0 \Leftrightarrow N_1 = \lambda N_0\]

Відтак, $\lambda = 1+r$. Значення $\lambda$ корисне, адже його можна використати для проекції розміру популяції на будь-якому кроці:

\[N_2 = \lambda N_1 = \lambda (\lambda N_0)\]

\[N_3 = \lambda N_2 = \lambda (\lambda N_1) = \lambda(\lambda[\lambda N_0])\]

І, у більш загальному випадку,

\[N_\tau = \lambda^\tau N_0\]

Такий ріст є прикладом геометричної прогресії, і, відтак, часто його називають геометричним ростом (geometric growth). Темп зростання популяції в такому випадку дорівнює $\frac{\Delta N}{\Delta \tau} = rN$, а темп зростання на особину – $\frac{\Delta N}{\Delta \tau \cdot N} = r$.

Модель геометричного росту є доволі простою, але передбачає дискретні кроки часу. В біологічній реальності, втім, процеси не відбуваються в чітко визначені часові межі: навіть якщо популяція тарганів походить від однієї самиці, навряд чи в третьому поколінні всі запліднені самиці відкладуть оотеку в той самий момент. Ні, скоріш за все, між особинами існуватиме певна варіація в часі. Коли популяції мають достатньо великий розмір, такі варіації в часі згладжуються і нагадують, скоріше, континуальний, а не дискретний процес. Відтак, геометричний ріст можливо переглянути в поняттях континуальних диференційних рівнянь.

Як ви пригадуєте, ідея диференційних рівнянь зводиться до оцінки зміни значення функції за дуже незначної зміни якоїсь змінної. В цьому випадку, змінною під питанням є час $\tau$, а отже ми розглядаємо такі зміни в популяції, що трапляються протягом безкінечно короткого часу, $\Delta \tau \rightarrow 0$. Якщо $\Delta \tau \rightarrow 0 = d\tau$ є дуже коротким кроком в часі, то й всі інші параметри ($N, b, d, r$) мають пропорційно зменшитись, чого можна досягнути якщо просто помножити їх на $\Delta \tau$. Тепер динаміку популяції можна уявити як диференційне рівняння

\[\frac{dN}{d\tau} = rN\]

Аби зрозуміти як $r$ і $\lambda$ пов’язані між собою в континуальному випадку, потрібно трохи пригадати інтегрування. Для початку, попереднє рівняння можна дещо перебудувати:

\[\frac{dN}{d\tau} = rN \stackrel{\cdot d\tau}{\Rightarrow} \frac{dN \cdot d\tau}{d\tau} = rN \cdot d\tau \stackrel{\div N}{\Rightarrow} \frac{dN}{N} = \frac{rN \cdot d\tau}{N} \Rightarrow \frac{1}{N}dN = r \cdot d\tau\]

Оскільки ці рівняння є диференційними, аби знайти чисельність популяції $N_\tau$ в момент часу $\tau = t$, їх необхідно проінтегувати: необхідно знайти $\int_{\tau=0}^{\tau=t} \frac{dN}{d\tau}$. Оскільки ми щойно з’ясували що

\[\frac{dN}{d\tau} = rN \Leftrightarrow \frac{1}{N}dN = r \cdot d\tau\]

то проінтегруймо обидва боки рівняння праворуч. По-перше,

\[\int\limits_{N = N_0}^{N = N_t} \frac{1}{N}dN = \left[ \ln |N| \right]_{N = N_0}^{N=N_t} = \ln(N_t) - \ln(N_0)\]

І, щодо другої частини

\[\int \limits_{\tau=0}^{\tau = t} r \cdot d\tau = r \int \limits_{\tau=0}^{\tau = t} d\tau = rt - 0 = rt\]

Отже, якщо тепер об’єднати обидва проінтегровані боки рівняння, то отримаємо

\[ \ln(N_t) - \ln(N_0) = rt \\ \ln(N_t) = \ln(N_0) + rt \\ N_t = N_0 \cdot e^{rt} \]

Такий ріст називається експоненційним ростом (exponential growth). Подібно до дискретного випадку, де $N_\tau = \lambda^\tau N_0$, параметр темпу росту популяції тепер можна визначити як $\lambda = e^r$, а, отже, $r = \ln(\lambda)$.

Експоненційний/геометричний ріст популяції часто ілюструють прикладом росту колонії бактерій на свіжому субстраті: з однієї клітини утворюється дві, з двох – чотири, з чотирьох – 8, далі 16, 32, 64, 128 і так далі. Нескладно помітити, що такий ріст прискорюється з часом (Рис. 4.2) – власне, чому він і називається експоненційним. І колонія бактерій, і нова популяція тарганів на кухні не може рости в такому темпі безкінечно довго, адже в якийсь момент доступні ресурси закінчуються і ефективне розмноження стає неможливим (а якби було можливим, то вже за декілька десятків поколінь вся планета була би вкрита шаром біомаси, чи то бактерій, чи то тарганів, на ваш вибір). Відтак, експоненційний ріст притаманний лише популяціям на початку колонізації за відносно низької щільності популяції, що можна спостерігати на ранніх стадіях біологічних інвазій (Arim et al. 2005) або у вимираючих видах, котрі повторно колонізують середовища в яких вони попередньо локально вимерли (Lavery et al. 1996). Особливістю експоненційного/геометричного росту є те, що темп росту популяції на особину є незалежним від щільності популяції (density-independent): і коли $N=1$, і коли $N \rightarrow \infty$, $\frac{\Delta N}{\Delta \tau \cdot N} = r$ та $\frac{d N}{d\tau \cdot N} = r$ – в правій частині цих рівнянь немає місця для $N$.

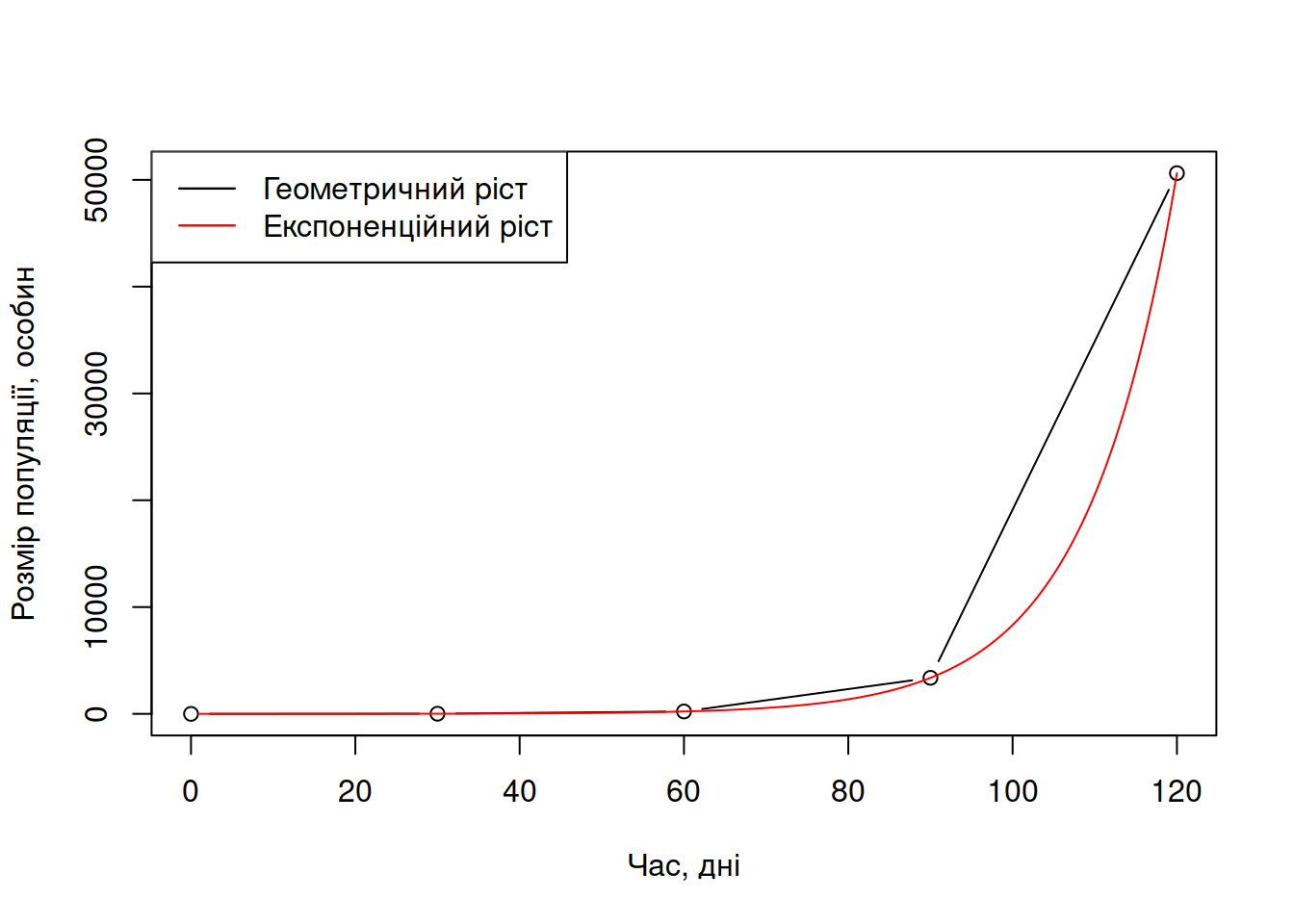
$Приклад (дискретного) геометричного та (континуального) експоненційного росту уявної популяції тарганів, в яких темп росту дорівнює $\lambda = 15$ кожні 30 днів.$

Рис. 4.2: Приклад (дискретного) геометричного та (континуального) експоненційного росту уявної популяції тарганів, в яких темп росту дорівнює $\lambda = 15$ кожні 30 днів.

Знання про модель експоненційного росту дозволяє провести цікавий трюк: аналітично знайти час, необхідний для подвоєння популяції. Визначмо $N_\tau = 2N_0$ (чисельність в якийсь момент часу дорівнює подвоєній чисельності вихідної популяції). Тоді, знаючи що $N_\tau = N_0 e^{r\tau}$, попередній вираз можна виразити як $2N_0 = N_0 e^{r\tau}$. Поділимо обидві частини на $N_0$, і знайдемо що $2 = e^{r\tau}$, звідки, знаючи про логарифми, можна розрахувати

\[ \ln2 = r\tau \\ \tau = \frac{ln2}{r} \]

Натуральний логарифм двійки є константою і дорівнює $\ln2 = 0.693\cdots$. Цей трюк іноді називають “правилом семидесяти”, адже час подвоєння популяції приблизно дорівнюватиме $0.70/r$.

4.6.2 Логістичний ріст

Звісно, для будь-якої популяції, чисельність якої зростає, справи не будуть завжди йти ідеально, і в якийсь момент експоненційний ріст повинен сповільнитись. Тому може бути безліч причин: (1) ресурси для популяції завжди обмежені, і в якийсь момент середовище просто не здатне прогодувати всіх особин в популяції⁵³; (2) поширення патогенів між особинами в щільних популяціях є дуже швидким, що спричинятиме епідемії із високою смертністю; (3) щільні популяції жертв спрощують полювання для хижака, який тепер витрачає менше енергії на полювання і може розмножитись за високої доступності жертв тощо. Аби зважити на це, необхідно якимось чином ввести залежність від щільності популяції (density-dependence). Якщо поглянути на експоненційну модель чисельності популяції

\[\frac{dN}{d\tau} = rN\]

то темп росту популяції, здається, зважений на чисельність популяції $N$ (ось же вона, $N$, в правій частині рівняння!), однак якщо розрахувати темп росту чисельності на особину (тобто поділити обидва боки рівняння на $N$), то побачимо, що експоненційний ріст ніяк не залежить від чисельності популяції – з перерахунку на особину, темп росту дорівнює константі $r$. Аби сповільнити ріст популяції із часом, нам необхідно додати якийсь член рівняння, який би був обернено пропорційний до чисельності популяції і, відтак, сповільнював її ріст. Тобто ми хочемо ввести негативний зв’язок між $N$ і $\frac{dN}{d\tau}$, і найпростіший спосіб це зробити – це визначити довільну максимальну чисельність популяції $K$. Значення $K$ називають ємністю середовища (carrying capacity), адже його можна уявити як максимальну чисельність популяції, яку може підтримувати ресурс середовища, виражену власне в кількості особин, а не в одиницях ресурсу чи інших параметрів самого середовища. Аби визначити обернену пропорційність, ми можемо ввести значення $\frac{N}{K}$ – воно наближається до нуля коли чисельність популяції $N$ є дуже маленькою відносно ємності середовища $K$, і наближається до одиниці коли $N \approx K$. Втім, в рівнянні динаміки чисельності популяції нам потрібен обернений ефект: щось, що не надто впливатиме на $r$ (тобто буде наближатись до одиниці) коли $N \rightarrow 0$, але зменшуватиме темп росту популяції (тобто множити $r$ на якесь число близьке до нуля) коли $N \rightarrow K$. Це дуже просто зробити через вираз $(1 - \frac{N}{K})$, і тепер рівняння динаміки популяції набуває вигляду

\[\frac{dN}{d\tau} = rN\left(1-\frac{N}{K}\right)\]

Відьмітьте, що якщо розмір популяції раптом перевищуватиме ємність середовища ($N > K$), то вираз $(1 - \frac{N}{K})$ набуватиме від’ємного значення, і, відтак, темп “росту” стане від’ємним – тобто популяція почне зменшуватись.

Таку динаміку росту популяції називають логістичним ростом (logistic growth), і розмір популяцій в будь-який момент часу $\tau = t$ можна знайти, подібно до експоненційного, через інтегрування виразу

\[\int \limits_{N = N_0}^{N=N_t} \frac{dN}{N} = \int \limits_{\tau = 0}^{\tau = t} r \left( 1 - \frac{N}{K}\right)d\tau\]

Рівняння логістичного росту трохи складніше, ніж експоненційного, але його все ще можна інтегрувати аналітично⁵⁴. Оскільки ми біологи, а не математики, аналітичне вирішення цього рівняння можна замінити за допомогою комп’ютерних обчислень, які, по суті, розділяють час на маленькі дискретні інтервали й шукають інтеграл як Рейманівську суму. Цей підхід можна звести до дискретного логістичного росту:

\[N_\tau = N_{\tau - 1} + rN_{\tau-1}\left( 1 - \frac{N_\tau}{K} \right)\]

Крива логістичного росту має характерну “S”-подібну форму (Рис. 4.3). На початкових етапах росту популяції ця крива нагадує експоненційний ріст – популяція збільшується швидше й швидше. Втім, оскільки з ростом популяції її розмір наближається до ємності середовища, темпи росту популяції починають зменшуватись, аж допоки вона повільно не наблизиться до ємності середовища. Від цього моменту часу чисельність популяції залишається стабільною, $N = K$.

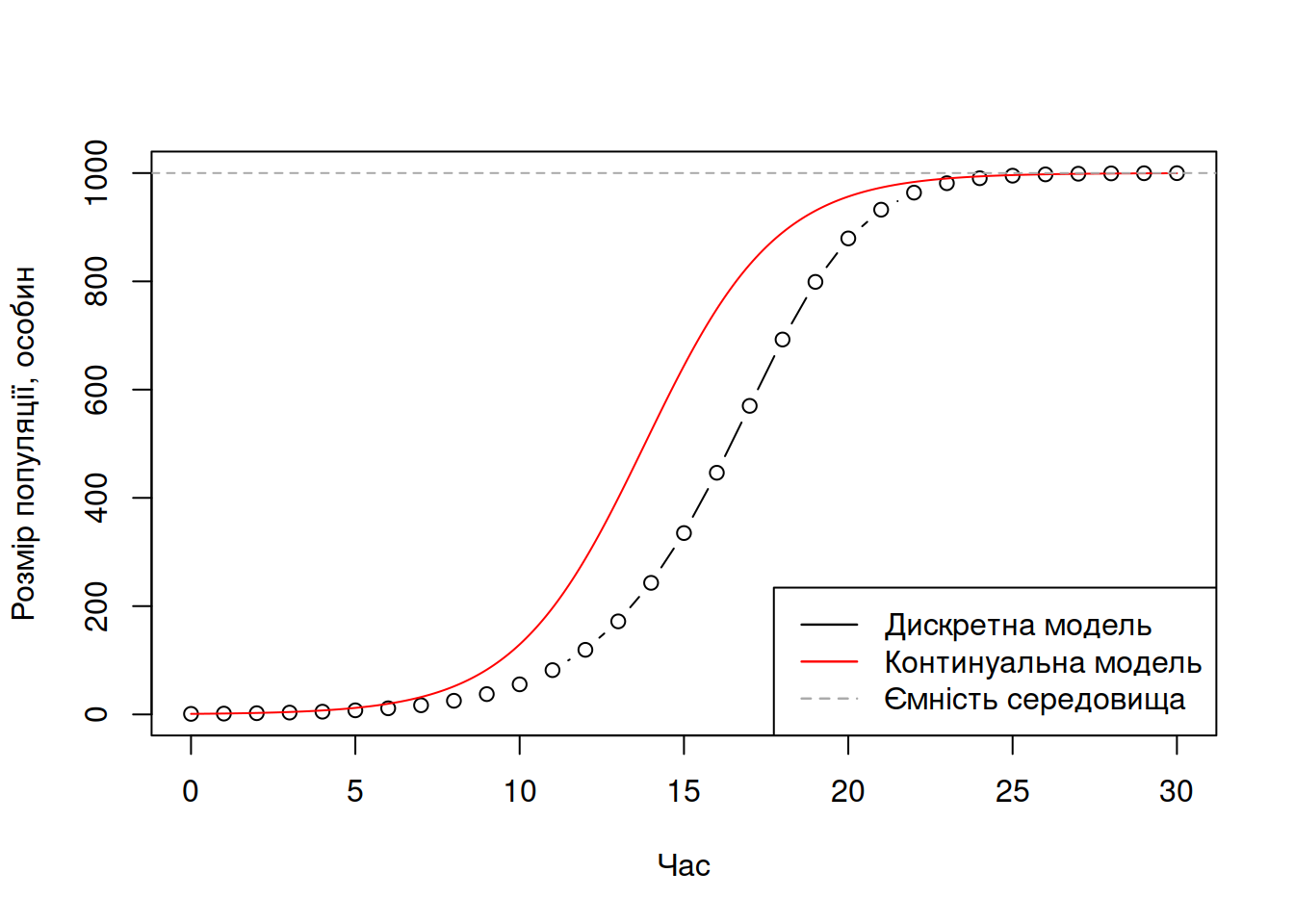
Рис. 4.3: Приклад дискретного та континуального логістичного росту за $r = 0.5, N_0 = 1, K = 1000$.

На Рис. 4.3 кидається в очі розбіжність між дискретною та континуальною моделлю, хоча їх параметри ($N_0, K, r$) начебто й є однаковими. Цю різницю можна пояснити природою дискретної моделі – між кроками в часі існує затримка. В будь-який довільний крок часу $\tau$, приріст популяції $(N_\tau - N_{\tau-1})$ визначається розміром популяції в минулий крок часу ($\tau-1$) – $N_{\tau-1}$. Натомість, для континуальної моделі приріст популяції визначається в кожний момент континуального часу, тобто в момент $\tau$, приріст популяції $\frac{dN}{d\tau}$ визначається для такого моменту $\tau - t$, що $t \rightarrow 0$, і, відповідно, поправка темпу росту популяції оцінюється не для розміру популяції цілу одиницю часу тому, а для майже поточного розміру популяції.

Останнім моментом щодо логістичного росту, на який варто звернути увагу, є залежність темпу росту від розміру популяції (Рис. 4.4). Питомий темп росту популяції (обчислений як сумарний приріст популяції в момент часу) збільшується із часом та кількістю особин в популяції, однак починає згасати після того, як розмір популяції сягає рівно половини від ємності середовища (Рис. 4.4-A,C). З іншого боку, темп росту популяції на особину (сумарний приріст популяції в момент часу поділений на розмір популяції в цей момент) є найбільшим на самому початку росту – адже в цей момент розмір популяції є найменшим (Рис. 4.4-B,D). Окільки ми бачимо чітку лінійну негативну залежність темпу росту на особину із кількістю особин в популяції, це знову доводить що логістичний ріст залежить від щільності популяції.

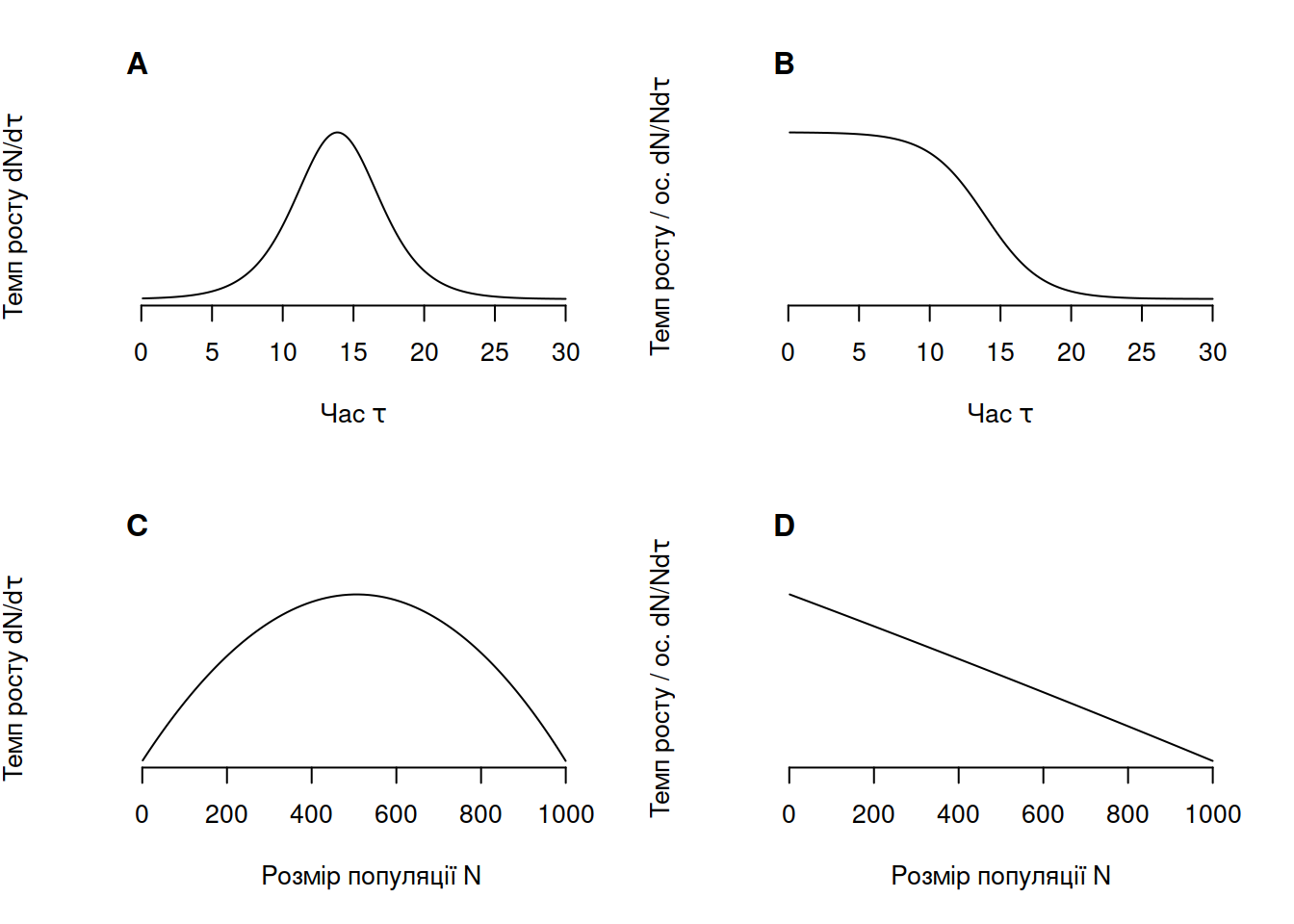
Зміна темпу росту популяції та темпу росту популяції на особину із часом та в залежності від розміру популяції в моделі континуального логістичного росту за $r = 0.5, N_0 = 1, K = 1000$.

Рис. 4.4: Зміна темпу росту популяції та темпу росту популяції на особину із часом та в залежності від розміру популяції в моделі континуального логістичного росту за $r = 0.5, N_0 = 1, K = 1000$.

Класично вважається, що залежність від щільності популяції можна знайти в усіх природних популяціях (Hairston et al. 1960). З іншого боку, докладний аналіз динаміки природних популяцій не показав доказів цієї залежності (Andrewartha & Birch 1954), що розпочало тривалу дискусію в екології. Деякі роботи вказують на те, що, зазвичай, чисельність популяцій флуктує з часом в щільність-незалежній манері (Dempster 1983), а залежність від чисельності вступає в гру тільки коли чисельність популяції є нетипово низькою чи нетипово високою. Наразі здається, що екологи дійшли компромісу: регуляція чисельності популяції здійснюється за рахунок і щільність-незалежних, і щільність-залежних механізмів залежно від ситуації, а самі дебати щодо залежності і незалежності ґрунтуються на математичних моделях популяцій, радше ніж біологічній реальності. Якими б зручними не були експоненційна чи логістична модель, вони є лише математичним апаратом для спрощення складної й багатовимірної дійсності, тому до висновків щодо динаміки популяції, які базуються на моделях, варто підходити із обережністю.

4.6.3 Модифікації логістичного росту

4.6.3.1 Максимальний сталий врожай

Для менеджменту біологічних популяцій логістична модель може допомогти в знаходженні максимального сталого врожаю (maximum sustainable yield) комерційно важливих диких популяцій (наприклад, риб, грибів, мисливських видів тощо). Наприклад, якщо припустити, що врожай особин лінійно пов’язаний із їх чисельністю (чим більше риби в озері, тим більше її виловлюють), то цю функцію можна об’єднати із щільність-залежною логістичною функцією росту популяції. Знаючи що найвищий темп росту популяції спостерігається за $N=K/2$ можна припустити, що ця чисельність популяції є оптимальною для сталого вилучення найбільшого об’єму особин із популяції, але це не зовсім так. Насправді, модифікований темп росту популяції складатиме

\[\frac{dN}{d\tau} = rN \left( 1-\frac{N}{K} \right) - yN\]

де $y$ – частка популяції, котра вилучається. Відтак, спочатку необхідно знайти залежність темпу росту популяції від розміру популяції ($dN = f(N)$, Рис. 4.4-C), і від неї відняти $yN$. Аби знайти оптимальне $y$, втім, можна прирівняти функцію прирісту популяції в рівнянні вище до нуля (адже $\frac{dN}{d\tau}$ є функцією від $N$), a $N$ – до $K/2$, і вирішити це для $y$ – в результаті⁵⁵ оптимальним значенням частки популяції, що підлягає вилученню, за якого темп росту популяції буде максимальним, становитиме $y = r/2$. На практиці, втім, менеджменту варто утримувати частку врожаю нижче за це значення аби напевне забезпечити стале відновлення популяції (Roughgarden & Smith 1996).

4.6.3.2 Ефект Аллі

Класичний логістичний ріст каже, що найвищий темп росту популяції на особину спостерігатиметься за найнижчої щільності особин. Відтак, всякий біолог повинен очікувати майже екпоненційного вибуху популяції, коли в ній лише декілька особин? Мабуть, що це не зовсім так: навпаки, за критично низької щільності популяції ми, навпаки, мусимо побоюватись вимирання такої популяції. Серед багатьох видів існує позитивний зв’язок між щільністю популяції та середньою пристосованістю особин, отже, за низької щільності особин ці особини мають низьку пристосованість, а, отже, й темп росту популяції за низької щільності буде низьким. Такий ефект відомий як ефект Аллі (Allee effect), і його можна пояснити декількома механізмами. Найпростіше пояснення працює для організмів, що розмножуються статево: низька щільність популяції ускладнює пошук статевого партнера і, відтак, успішної копуляції (якщо у вас є дуже великий акваріум і дві маленькі різностатеві рибки, то, можливо, вони ніколи не знайдуть одна одну в цьому великому акваріумі). Такий механізм поширений в багатьох системах від популяцій рослин до великих ссавців (Berec et al. 2007). Альтернативні механізми можуть включати надмірну експлуатацію популяцій людиною (Courchamp et al. 2006), залежність виживання від включення у великі соціальні групи (Courchamp & Macdonald 2001), вищу індивідуальну вразливість до хижацтва серед малих груп жертви (Wittmer et al. 2005), залежність від кооперативного захисту від хижаків (Clutton-Brock et al. 1999), зміну умов середовища на більш сприятливі для майбутнього потомства (Rinell et al. 2011) тощо, при чому різні механізми ефекту Аллі можуть перекриватись в одній системі (Berec et al. 2007).

Математично, ефект Аллі можна додати до рівняння логістичного росту наступним чином:

\[\frac{dN}{d\tau} = rN \left( 1 - \frac{N}{K} \right) \left( 1 - \frac{A}{N}\right)\]

де $A$ відповідає критичному розміру популяції, нижче за який темпи росту популяції стають негативними (Рис. 4.5). Позитивний приріст популяції можливий лише коли $A > N > K$.

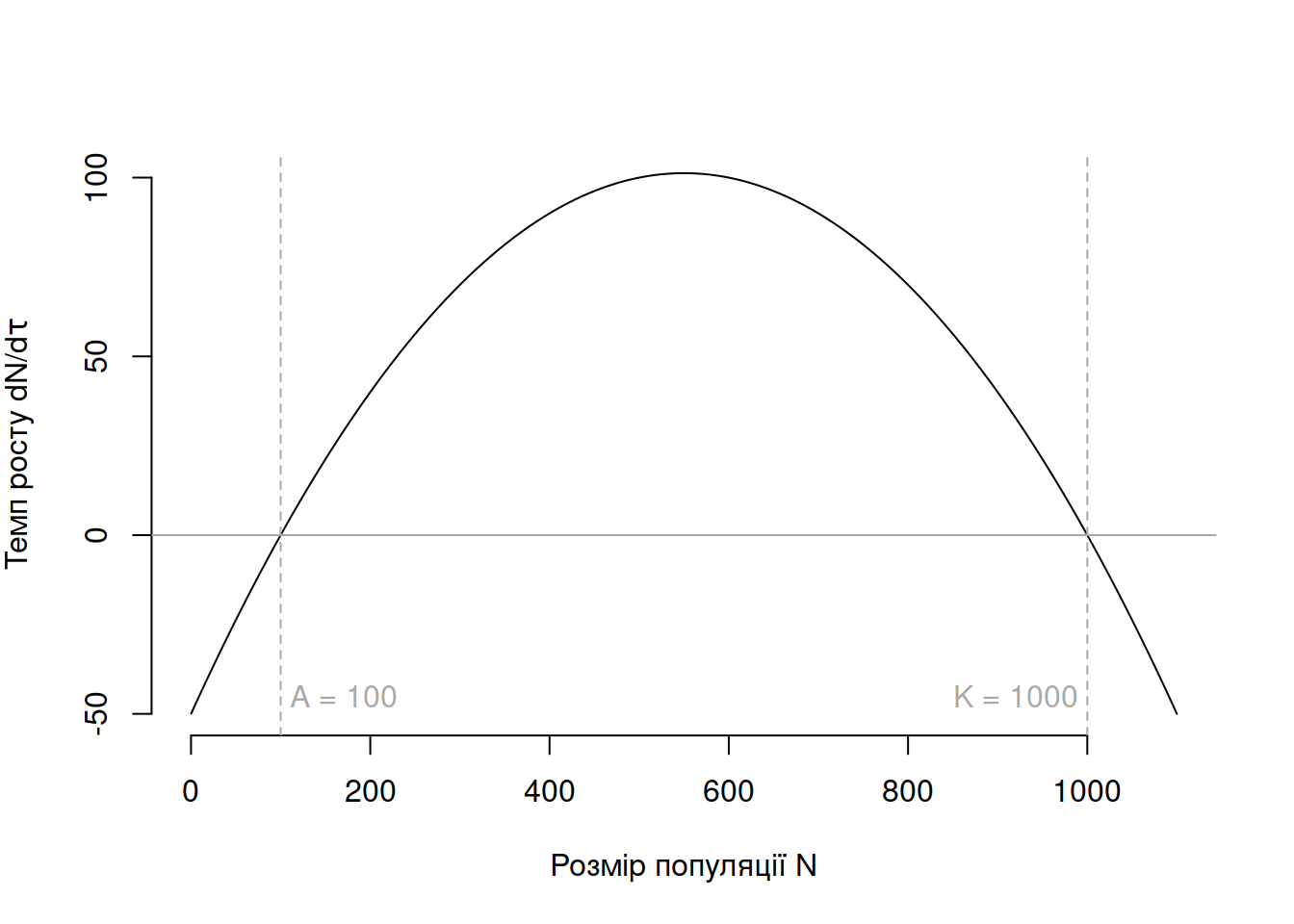
Рис. 4.5: Ефект Аллі на логістичний темп росту популяції за $r = 0.5, K = 1000$ та критичного розміру популяції $A = 100$.

4.6.3.3 Тета-логістичний ріст

Нарешті, цікавою модифікацією логістичної моделі є модель тета-логістичного росту (theta-logistic growth), окремим випадком якої є логістичний ріст. Тета-логістична модель є більш загальною й надає додаткову гнучкість в моделюванні, й має форму

\[\frac{dN}{d\tau} = rN \left( 1 - \left( \frac{N}{K} \right)^\theta \right)\]

Новий параметр $\theta$ дозволяє змінювати форму зв’язку між розміром популяції та темпом росту на особину. Наприклад, коли $\theta = 1$ і тета-логістичний ріст має форму звичайного логістичного росту, розмір популяції лінійно визначає темп росту популяції на особину (Рис. 4.4-D) – однак цей зв’язок в природі може бути нелінійним. Зміна значення $\theta$ й додає таку нелінійність. Наприклад, якщо $\theta > 1$, за низької щільності популяції вплив щільність-залежних механізмів зменшується. Така модель дозволяє моделювати баланс між щільність-залежною та щільність-незалежною регуляцією чисельності популяції (Sibly et al. 2005).

4.6.4 Динаміка та стабільність популяції

Популяції є динамічними системами, адже вони змінюються з часом. Розглянуті вище математичні моделі також є динамічними системами, і якими б спрощеними відображеннями реальності вони не були, має зміст розглянути динаміку та стабільність популяцій з математичної точки зору.

В математиці існує поняття точки рівноваги (equilibrium point), яке має складне визначення з купою математичних нотацій, в яке ми не будемо лізти. На наше щастя, математична рівновага має наслідки в багатьох більш практичних сферах, наприклад, в механіці. Ми спробуємо уявити екологічні системи через аналогії із механічними системами. Якщо уявити м’ячик на нахиленій поверхні, такий м’ячик буде завжди в динамічному стані руху і ніколи не досягне рівноважного стану (Рис. 4.6-A). На рівній поверхні ж м’ячик буде в стані спокою, однак за найменшого впливу на цю систему позиція м’ячика змінюватиметься, і не можна визначити жодної точки, в якій ця система залишиться (Рис. 4.6-В) – хоча й вона перебуває в стані рівноваги допоки на неї не діють зовнішні сили. Стан нестійкої рівноваги (Рис. 4.6-С) начебто і знаходиться в рівновазі, але щойно до неї застосується найменша зовнішня сила – і м’ячик одразу злетить зі свого випуклого постаменту. Нарешті, за стійкої рівноваги (Рис. 4.6-D), система завжди тяжіє до певного стану, і навіть якщо її тимчасово вивести із рівноваги, вона до цього стану повернеться. В цьому випадку, ми називаємо найнижчу точку субстрату, до якої м’ячик зажди тяжіє, атрактором (attractor) – станом, до якої система тяжіє змінитись. Система може мати більше ніж один альтернативний атрактор (Рис. 4.6-E,F).

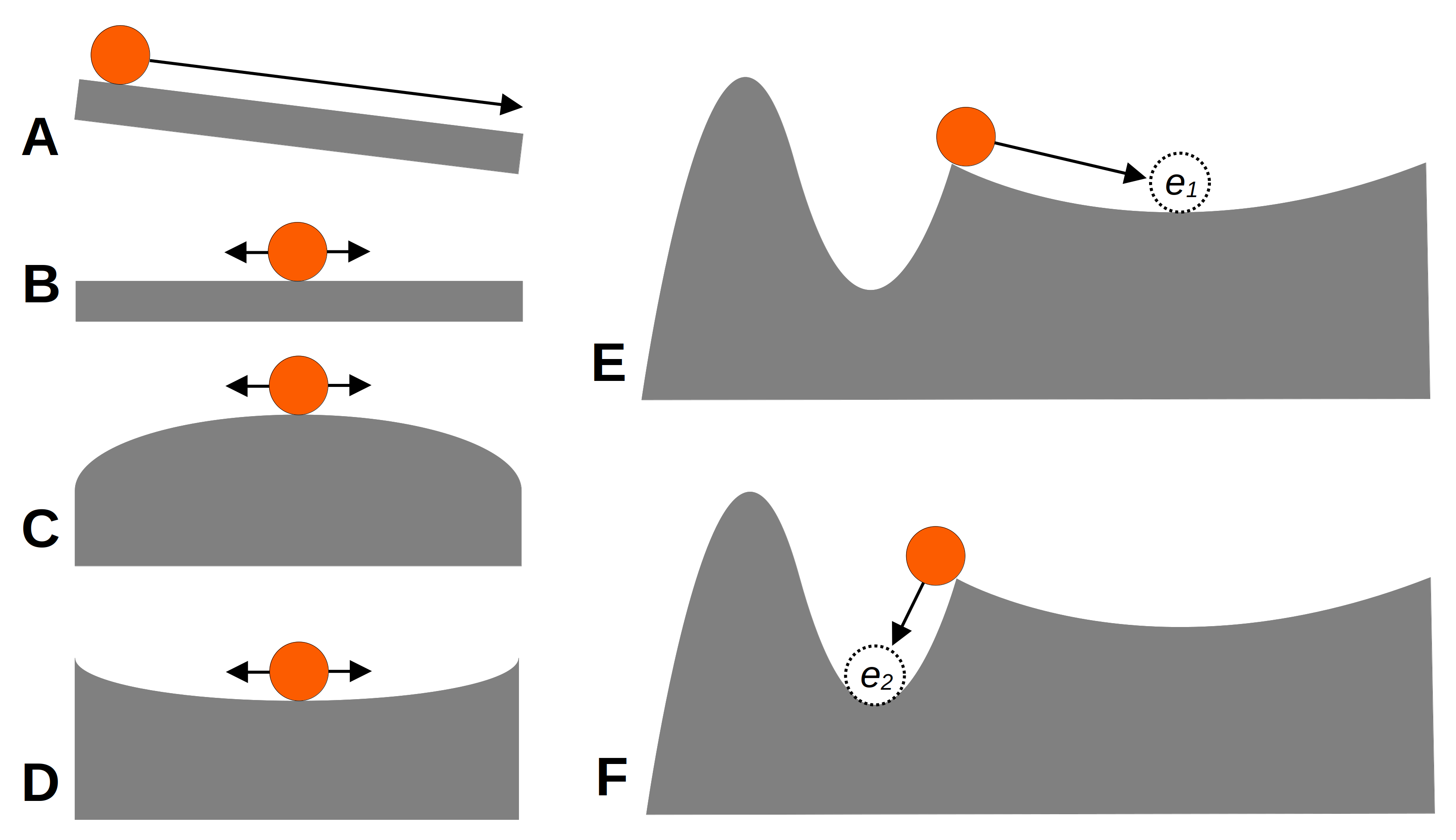
Схематичне відображення різних сценаріїв рівноваги в системі: (**A**) система не є рівноважною; (**B**) система в нейтральній рівновазі; (**С**) система в нестійкій рівновазі; (**D**) система в стійкій рівновазі; (**E-F**) два альтернативні рівноважні стани, де атрактор системи $e_1$ може змінитись на атрактор $e_2$ залежно від початкового стану системи і сили, із якою систему виводять із рівноваги.

Рис. 4.6: Схематичне відображення різних сценаріїв рівноваги в системі: (A) система не є рівноважною; (B) система в нейтральній рівновазі; (С) система в нестійкій рівновазі; (D) система в стійкій рівновазі; (E-F) два альтернативні рівноважні стани, де атрактор системи $e_1$ може змінитись на атрактор $e_2$ залежно від початкового стану системи і сили, із якою систему виводять із рівноваги.

У випадку логістичного росту популяції, система є динамічною, адже чисельність популяцій змінюється із часом, однак в цій системі існує атрактор: щойно чисельність популяції досягає ємності середовища $K$, система досягає стану стійкої рівноваги $N=K$. Що стається, якщо щось порушує цю рівновагу (наприклад, сталася несподівана катастрофічна подія яка знищила якусь частку особин в популяції, або хтось штовхнув м’ячик на Рис. 4.6-D)? Система має повернутись до стану рівноваги, і математичні методи дозволяють оцінити характерний час повернення до рівноваги (characteristic return time) як $\frac{1}{r}$,⁵⁶ а, відтак, характерний темп повернення до рівноваги (characteristic return rate) дорівнюватиме $r$. Для дискретних систем, точка рівноваги є стабільною тільки якщо $0 < r < 2$ (May et al. 1974).

У своїй класичній роботі 1974-го року, математичний еколог Роберт Мей показав як прості дискретні моделі логістичного росту популяції можуть замість стану рівноваги досягати стабільних періодичних циклів (limit cycles), коли розмір популяції із часом стрибає між двома значеннями. Ба більше, за певних параметрів моделі атракторів стає все більше, і дуже швидко ріст популяції стає хаотичним⁵⁷. Розгляньмо, як різні значення $r$ впливають на рівновагу популяції в дискретній логістичній моделі:

Code

library(tidyverse)

# визначимо функцію дискретного логістичного росту
logistic_discrete <- function(N, r, K = 1000){
  N + N*r*(1 - (N/K))
}

# ініціалізуємо вихідний датасет
logistic_rates <- tibble()

# визначимо набір значень внутрішнього темпу росту
IGRs <- seq(from = 0.1, to = 2.9, by = 0.0025) %>% 
  round(digits = 3)

steps <- 1000 # кількість кроків в кожній симуляції

for (r in IGRs){ # для кожного значення внутрішнього темпу росту...
  # ... ініціалізуємо вектор чисельностей на кожному кроці
  n <- numeric(steps)
  # ... чисельність на початку симуляції - одна особина
  n[1] <- 1
  for (i in 2:steps){ # для кожного кроку в часі...
    n[i] <- logistic_discrete(N = n[i-1], r = r)
  }
  # запишемо результат симуляції
  logistic_rates <- bind_rows(
    logistic_rates,
    tibble(
      n = n, 
      r = r
    ) %>% rowid_to_column(var = "time")
  )
}

# побудуймо графік для вибраних значень внутрішнього темпу росту
logistic_rates %>% 
  filter(time < 100,
         r %in% c(1.9, 2.1, 2.9)) %>%
  ggplot(aes(x = time, y = n, color = as.factor(r))) + 
  geom_line(alpha = 0.7) +
  xlab("Час") + 
  ylab("Чисельність, ос.") +
  labs(color = "r")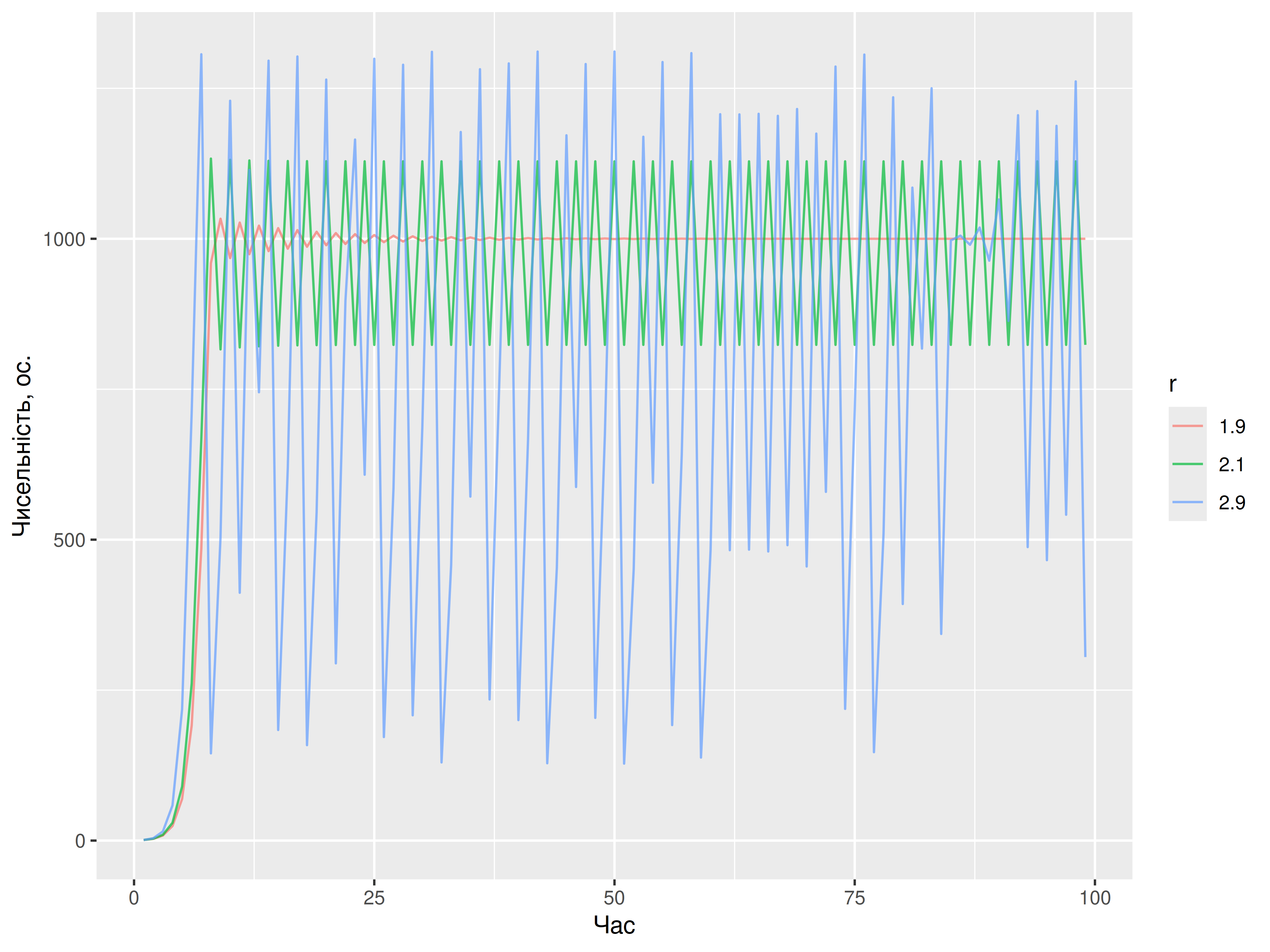

Ми бачимо, що за $r = 1.9$, популяція росте дуже швидко і в якийсь момент перевищує ємність середовища ($K = 1000$). Після цього, ріст популяції стає від’ємним, адже вона має зменшити свій розмір до $N \leq K$. Якийсь час чисельність популяції коливається навколо атрактора $K$, аж допоки система не досягає стану рівноваги. Коли ж $r = 2.1$, популяція входить в стан стабільних періодичних циклів, і чисельність популяції регулярно коливається між двома значеннями. За $r = 2.9$ система стає зовсім хаотичною, і виглядає, ніби значення чисельності популяції на кожному кроці ніяк не можна передбачити. Власне, Мей (1974-го року(https://doi.org/10.1126/science.186.4164.645)) виявив, що за $0 < r < 2$, дискретна логістична модель має один атрактор, але їх кількість збільшується до двох-атракторного стабільного циклу за $r > 2$, і далі до чотирьох, восьми, 16, 32 атракторів, і допоки система не містить хаотичні атрактори. Із попереднім прикладом, ми можемо візуалізувати атрактори, якщо ігноруватимемо всі моменти часу, коли популяція ще росте – виглядає, що фаза росту спостерігається лише протягом перших десятків-двох кроків. Суто заради консервативності, викиньмо перші 150 кроків з усіх симуляцій.

Code

logistic_rates %>% 
  filter(time > 150) %>%
  filter(r > 1.8) %>%
  ggplot(aes(x = r, y = n)) +
  geom_point(size = 0.2, alpha = 0.75, stroke = 0) +
  xlab("Внутрішній темп росту r") +
  ylab("Атрактор N")

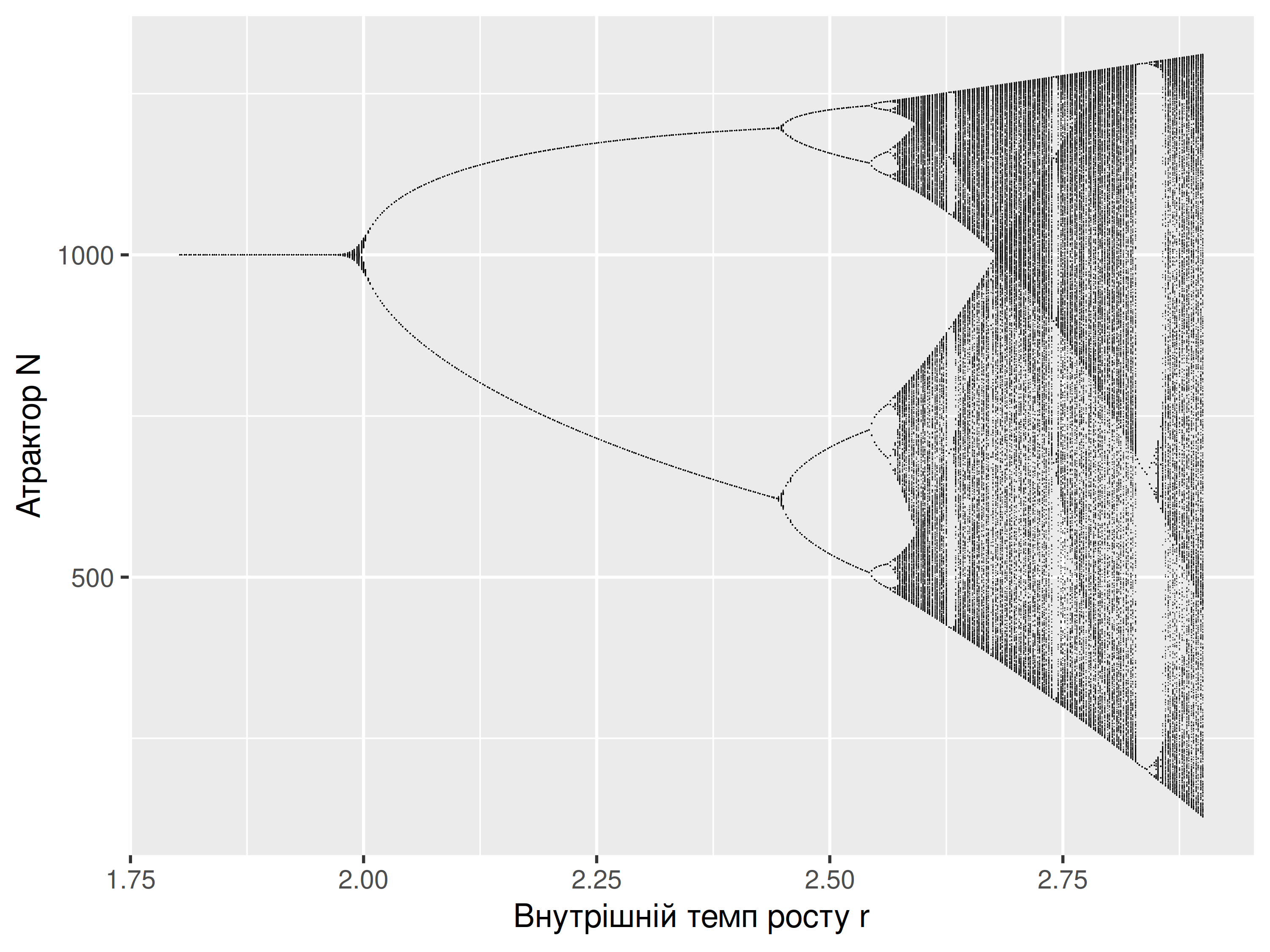
Ця мапа отримала назву біфуркаційної діаграми (bifurcation diagram) і є відомим візуальним відображенням хаотичного процесу. Отримання дуже складних, хаотичних результатів із дуже простих моделей свого часу додало палива до дискусії щодо того, чи варто вірити моделям щільність-залежного росту, адже досі незрозуміло чи реальні біологічні популяції мають властивості динамічних систем в стані рівноваги (Turchin 1995). Стабільні періодичні цикли та хаотичні атрактори вчать досвідчених екологів хорошого уроку щодо динаміки популяцій: навіть якщо розмір популяції коливається із часом, це не завжди вказує на спрямовані зміни, але може бути наслідком періодичних коливань. Відтак, варто бути обережними щодо спостереженої динаміки популяції: в найгіршому випадку, якщо чисельність популяції спостережена в часі лише декілька (щонайменше двічі) разів, дуже легко можна зробити хибний висновок про збільшення чи зменшення розміру популяції навіть коли вона, насправді, стабільна.

Загалом, до динаміки популяції в часі завжди варто ставитись як до часових серій (time series) із застосуванням відповідних статистичних методів. Наприклад, статистика Дікі-Фуллера (Dickey–Fuller test) може бути хорошим початковим кроком до з’ясування, чи популяція є стабільною в часі. З іншого боку, використання параметричних статистик на кшталт коефіцієнту варіації чи лінійної регресії з часом є дуже небезпечним підходом, адже більшість статистичних підходів передбачає вибірку незалежних спостережень. А якщо цей розділ вас чогось і навчив, то я дуже сподіваюсь, що спостереження чисельності в часі на кшталт $N_\tau = N_{\tau-1} + f(N_{\tau-1})$ виглядає як що завгодно, але не як незалежні спостереження.

Припустімо, одна оотека має 30 яєць, і половина із них вилуплюється самицями: із першого покоління ми маємо 15 самиць (15×2 = 30 особин), кожна з яких відкладе 30 яєць (15×30 = 450 особин), із яких половина самиць (тобто 225 самиць), що означає 225×30 = 6,750 яєць в наступному поколінні.↩︎
Мальтузіанська катастрофа описує ситуацію, в якій ріст популяції із часом експоненційний, а ріст доступного ресурсу – лінійний. В якийсь момент ці дві функції перетнуться, після чого розмір популяції перевищуватиме об’єм доступного ресурсу, що спричинятиме голод і подальший колапс популяції. Ця концепція переважно застосовується до людської популяції, і разом з голодом передбачає інші соціальні кризи на кшталт війни (Arrow et al. 2004).↩︎
Спочатку змінимо вихідне рівняння як \[\frac{dN}{d\tau} = rN \left( 1 - \frac{N}{K} \right) \stackrel{\cdot d\tau}{\Rightarrow} dN = rN \left(1 - \frac{N}{K} \right)d\tau \Rightarrow \\ \Rightarrow d\tau = \frac{1}{rN(1 - \frac{N}{K})} dN \stackrel{\cdot r}{\Rightarrow} r \cdot d\tau = \frac{1}{N(1-\frac{N}{K})}dN\] Ми вже знаємо що $\int_{\tau=0}^{\tau = t} r \cdot d\tau = rt$, тож нам необхідно проінтегрувати лише праву частину: \[\int \limits_{N_0}^{N_t} \frac{1}{N(1-\frac{N}{K})} dN = \int \limits_{N_0}^{N_t} \frac{1}{N - \frac{N^2}{K}}dN = -K \int \limits_{N_0}^{N_t} \frac{1}{N^2 - KN}dN = \\ = -1 \int \limits_{N_0}^{N_t} \frac{K}{(1 - \frac{K}{N}) N^2} dN \stackrel{u = 1 - \frac{K}{N} \Rightarrow du = \frac{K}{N^2}dN}{=} -1 \int \limits_{N_0}^{N_t} \frac{1}{u} du = \\ = -1 \left[ \ln (u) \right]_{N_0}^{N_t} = -1 \left[ \ln \left( 1 - \frac{K}{N} \right) \right]_{N_0}^{N_t} = - \ln \left( 1-\frac{K}{N_t} \right) + \ln \left( 1-\frac{K}{N_0} \right)\] Відтак, тепер можна об’єднати обидві частини рівняння і вирішити для $N_t$: \[\ln \left( 1-\frac{K}{N_0} \right) - \ln \left( 1-\frac{K}{N_t} \right) = rt \\ \ln \left( 1-\frac{K}{N_t} \right) = \ln \left( 1-\frac{K}{N_0} \right) - rt \\ 1 - \frac{K}{N_t} = \left( 1 - \frac{K}{N_0} \right) e^{-rt} \\ \frac{K}{N_t} = 1 - \left( 1 - \frac{K}{N_0} \right) e^{-rt} \\ N_t = \frac{K}{1 - (1 - \frac{K}{N_0}) e^{-rt}}\]↩︎
Визначмо $\frac{dN}{d\tau} = rN(1-\frac{N}{K}) - yN$, яке ми прирівняємо до нуля і замінимо $N = K/2$, тоді \[0 = r \frac{K}{2}(1 - \frac{K}{2K}) - y \frac{K}{2} = r \frac{K}{2}(1 - \frac{1}{2}) - y \frac{K}{2} = \frac{1}{2} \frac{K}{2}r - y \frac{K}{2}\] Вирішимо для $y$: \[\frac{K}{2}y = \frac{1}{2} \frac{K}{2} r \Rightarrow y = r \frac{1}{2} \frac{K}{2} \cdot \frac{2}{K} = \frac{1}{2}r\]↩︎
Приймемо, що в точці рівноваги $N = K$, тоді ми можемо розрахувати часткову похідну темпу росту для розміру популяції, \[\frac{\partial \left( rN (1 - \frac{N}{K}) \right)}{\partial N} = \frac{\partial \left( rN- \frac{rN^2}{K} \right)}{\partial N} = r - \frac{2rN}{K}\] В цьому рівнянні можна замінити $N$ на $K$ і отримати \[r - \frac{2rN}{K} = \stackrel{N = K}{=} r - \frac{2rK}{K} = r - 2r = -r\] Отже, зміна приросту популяції поблизу точки рівноваги зі зміною в розмірі популяції пов’язана лінійно й негативно із нахилом $r$. Коли популяція знаходиться в рівновазі, стохастичне збурення в чисельності популяції можна уявити як невеличку зміну чисельності $n$, тобто в якийсь момент часу розмір популяції становитиме $N + n$. Темп зміни збурення із часом тоді становитиме $\frac{dn}{d\tau} = -rn$, що відповідає негативному експоненційному росту, або експоненційному затиханню (exponential decay). Оскільки ми вже вивели рівняння експоненційного росту, рівень збурення можна передбачити як $n_\tau = n_0 e^{-r\tau}$. За скільки часу збурення затихне остаточно? Оскільки збурення має функцію експоненційного затихання, воно ніколи не досягне нуля. Натомість, ми можемо оцінити час, за який збурення затихне до рівня $1/e$: \[n_\tau = \frac{n_0}{e} = n_0 e^{-r\tau} \Rightarrow \\ \Rightarrow n_0 e^{-1} = n_0 e^{-r\tau} \Rightarrow \ln(n_0 e^{-1}) = \ln(n_0 e^{-r\tau}) \Rightarrow n_0 - 1 = n_0 - r\tau \Rightarrow \\ \Rightarrow -r\tau = n_0 - n_0 - 1 \Rightarrow \tau = \frac{-1}{-r} = \frac{1}{r}\]↩︎
Хаос (chaos) – поведінка детерміністичної системи, за якої найменші зміни вхідних параметрів не дозволяють апроксимувати розвиток системи. Зазвичай, хаотична система описується дуже високою чутливістю до початкових параметрів системи, не-періодичністю тощо. Помітьте, що якщо значення вхідних параметрів ідентичне, то й результати будуть ідентичними – хаос стосується лише непередбачуваності системи за найменшої зміни параметрів.↩︎