3.2 Лінійна алгебра

3.2.1 Визначення матриці

Матриця є двовимірним набором значень, що позначається як

\[\textbf{A} = \begin{bmatrix} a_{1, 1} & a_{1,2} & \cdots & a_{1, n}\\ a_{2, 1} & a_{2,2} & \cdots & a_{2, n}\\ \vdots & \vdots & a_{i,j} & \vdots \\ a_{m, 1} & a_{m,2} & \cdots & a_{m, n} \end{bmatrix}\]

в якій $i: 1, 2, \cdots, m-1, m$ позначає індекс рядка елементу і $j: 1, 2, \cdots, n-1, n$ позначає індекс колонки елементу $a_{i, j}$. В цій книзі матриці як об’єкти позначатимуться жирними великими літерами і визначатимуться як матриці в квадратних дужках, але варто мати на увазі, що позначення іноді варіюють в різних джерелах.

Розмірність матриці визначається кількістю рядків $m$ та кількістю колонок $n$. Якщо один із цих вимірів дорівнює одиниці, матриця являє собою вектор – послідовність значень. Поняття вектору важливе для розуміння оперування даними, адже спостереження (рядки) та параметри (колонки) в масиві даних є векторами розмірністю $m \times 1$ або $1 \times n$. Вектори позначаються як $\vec{a}$.

В подальшому матриці визначені як жирні літери (напр., $\mathbf{A}$), а елементи матриці – як індексовані літери $a_{i,j}$, або $[\mathbf{A}]_{i,j}$.

3.2.2 Трансформації матриць

Додавання матриць, якщо обидві матриці мають ідентичну розмірність, є доволі очевидним, адже додаються елементи із ідентичними індексами. Наприклад, $\mathbf{A}+\mathbf{B} = a_{i,j}+b_{i, j}$.

Наприклад, якщо

\[\mathbf{A} = \begin{bmatrix} a_{1, 1} & a_{1,2} & \cdots & a_{1, n}\\ a_{2, 1} & a_{2,2} & \cdots & a_{2, n}\\ \vdots & \vdots & a_{i,j} & \vdots \\ a_{m, 1} & a_{m,2} & \cdots & a_{m, n} \end{bmatrix}, \mathbf{B} = \begin{bmatrix} b_{1, 1} & b_{1,2} & \cdots & b_{1, n}\\ b_{2, 1} & b_{2,2} & \cdots & b_{2, n}\\ \vdots & \vdots & b_{i,j} & \vdots \\ b_{m, 1} & b_{m,2} & \cdots & b_{m, n} \end{bmatrix}\]

тоді

\[\mathbf{A} + \mathbf{B} = \begin{bmatrix} a_{1, 1}+b_{1, 1} & a_{1,2}+b_{1,2} & \cdots & a_{1, n}+b_{1, n}\\ a_{2, 1}+b_{2, 1} & a_{2,2}+b_{2,2} & \cdots & a_{2, n}+b_{2, n}\\ \vdots & \vdots & a_{i,j}+b_{i,j} & \vdots \\ a_{m, 1}+b_{m, 1} & a_{m,2}+b_{m,2} & \cdots & a_{m, n}+b_{m, n} \end{bmatrix}\]

Подібно до додавання, скалярне множення матриць полягає в отриманні добутку константи із кожним елементом матриці:

\[c \cdot \mathbf{A} = c \cdot a_{i, j} = \begin{bmatrix} c \cdot a_{1, 1} & c \cdot a_{1,2} & \cdots & c \cdot a_{1, n}\\ c \cdot a_{2, 1} & c \cdot a_{2,2} & \cdots & c \cdot a_{2, n}\\ \vdots & \vdots & c \cdot a_{i,j} & \vdots \\ c \cdot a_{m, 1} & c \cdot a_{m,2} & \cdots & c \cdot a_{m, n} \end{bmatrix}\]

Нарешті, транспонування матриці полягає в заміні індексування рядків та колонки і навпаки, $i \rightarrow j, j \rightarrow i$, тобто,

\[\mathbf{A'} = \mathbf{A^T} = a'_{j, i} \text{ } \forall \text{ } \mathbf{A} = a_{i, j}\]

3.2.3 Операції над матрицями

Множення матриць є дещо складнішим, і загальним правилом є те, що для матриць $A$ розміром $m \times n$ і $B$ розміром $n \times p$ добуток складатиме матрицю розміром $m \times p$ (відповідно, кількість колонок в першій матриці повинна дорівнювати кількості рядків в другій матриці) із елементами, що відповідають сумі добутків рядків $A$ та колонок $B$, тобто елемент добутку матриць із індексами $i, j$ складатиме (Bogacki 2019) (Рис. 3.7)

\[[\mathbf{AB}]_{i, j} = \sum \limits_{r=1}^n (a_{i,r} b_{r, j}) = a_{i,1} b_{1, j} + a_{i, 2}b_{2, j} + \cdots + a_{i, n}b_{n, j}\]

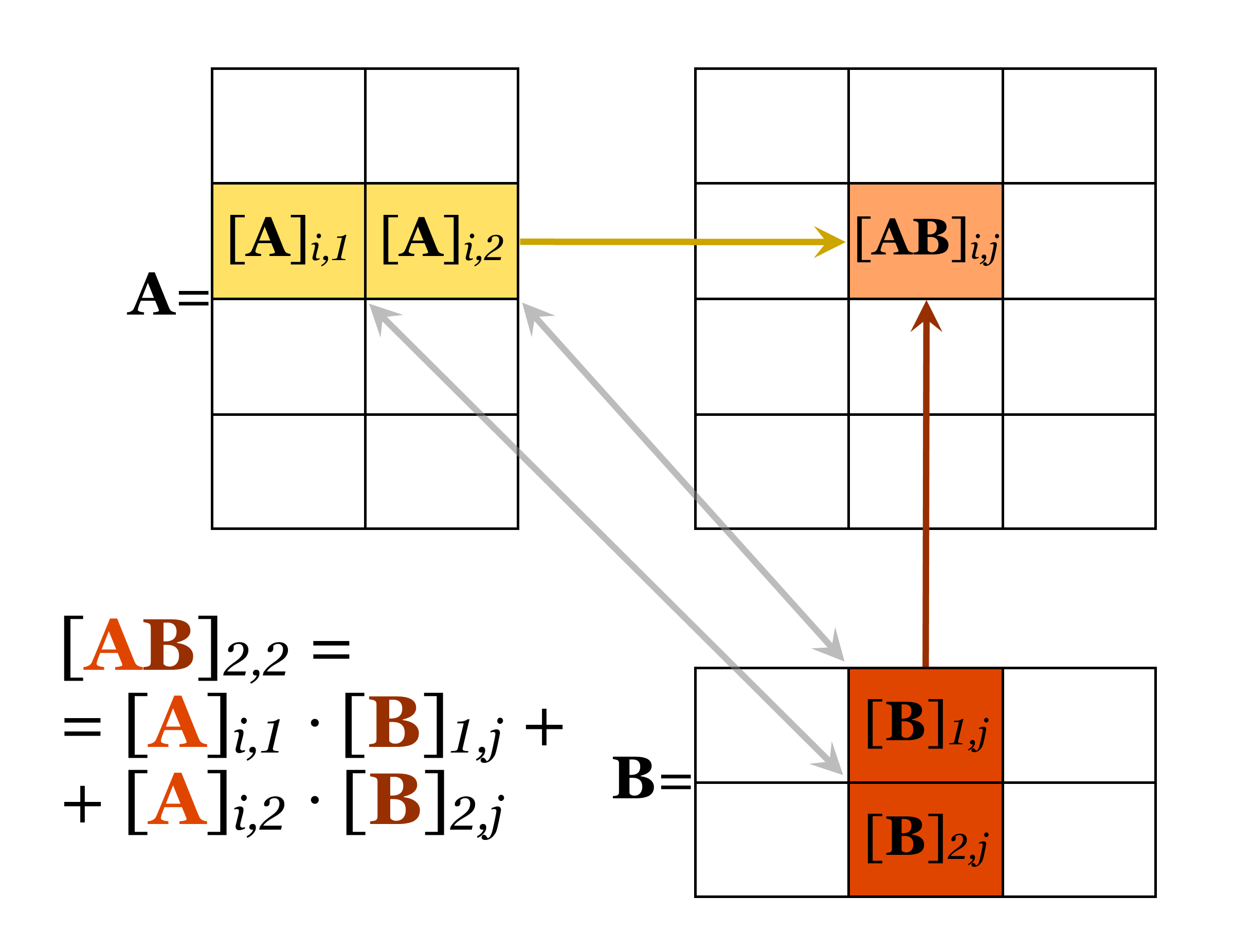
$Знаходження значення елементу добутку матриць $\mathbf{A}$ і $\mathbf{B}$.$

Рис. 3.7: Знаходження значення елементу добутку матриць $\mathbf{A}$ і $\mathbf{B}$.

За додавання матриць завжди потрібно враховувати розмірність матриць. Якщо матриця $\mathbf{A}$ має розмір $m \times n$, друга матриця $\mathbf{B}$ має розмір $n \times p$, то їх добуток $\mathbf{AB}$ матиме розмір $m \times p$. Відтак, для множення матриць необхідно, аби кількість колонок першої матриці дорівнювала кількості рядків другої матриці.

Для добутків матриць властиво, що

\[\mathbf{AB} \neq \mathbf{BA}\]

\[(\mathbf{AB})\mathbf{C} = \mathbf{A}(\mathbf{BC})\]

\[(\mathbf{A+B})\mathbf{C} = \mathbf{AC} + \mathbf{BC}\]

\[\mathbf{C}(\mathbf{A+B}) = \mathbf{CA} + \mathbf{CB}\]

Очевидно, що якщо множення матриць можливе, то можливо також і звести матрицю в ступінь, наприклад,

\[\mathbf{A}^3 = (\mathbf{AA})\mathbf{A}\]

Уявімо квадратну одиничну матрицю $\mathbf{I}_n$ розміром $n \times n$, де

\[\mathbf{I}_n = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots &\vdots \\ 0 & 0 & 0 & \cdots & 1 \end{bmatrix}\]

тобто всі, крім діагональних, елементи матриці дорівнюють нулю. Тоді

\[\mathbf{AB} = \mathbf{I}_n = \mathbf{BA}\]

отже, $\mathbf{B}$ є оберненою матрицею $\mathbf{A}$:

\[\mathbf{B} = \mathbf{A}^{-1}\]

\[\mathbf{AA^{-1}} = \mathbf{I}_n\]

\[\mathbf{A}^0 = \mathbf{I}_n\]

Не для будь-якої матриці може існувати обернена матриця.

Подібно до математичних функцій, лінійні трансформації можуть приймати вектори чи матриці в якості аргументу:

\[F: \mathbb{R}^n \rightarrow \mathbb{R}^m \text{ якщо}\]

\[F(\vec{u} + \vec{v}) = F(\vec{u}) + F(\vec{v}) \text{ } \forall \text{ } \vec{u}, \vec{v}\]

\[F(c \vec{u}) = c F(\vec{u}) \text{ } \forall \text{ } \vec{u}, c\]

\[F(c_1 \vec{u_1} + \cdots + c_k \vec{u_k}) = c_1 F(\vec{u_1}) + \cdots + c_k F(\vec{u_k})\]

\[F: \mathbb{R}^n \rightarrow \mathbb{R}^m \iff \exists \mathbf{A}: F(\vec{v}) = \mathbf{A} \vec{v}, \mathbf{A} = a_{i, j}, 1 < i<m, 1 < j < n\]

3.2.4 Детермінант, власні вектори, та власне значення

Детермінант визначається (Bogacki 2019) для матриці $1 \times 1$ $\mathbf{A} = [a_{1, 1}]$ як

\[\det \mathbf{A} = a_{1, 1}\]

і для більших квадратних матриць розміром $n \times n$ рекурсивно

\[\det \mathbf{A} = \sum \limits_{j=1}^n (-1)^{1+j} a_{1, j} \det \mathbf{M}_{1,j}\]

де $\mathbf{M}_{i,j}$ є підматрицею від $\mathbf{A}$ розміром $(n - 1) \times (m - 1)$ із видаленими рядком $i$ і колонкою $j$, тобто,

\[\det \mathbf{A} = a_{1,1} \det \mathbf{M}_{1,1} - a_{1,2} \det \mathbf{M}_{1,2} + a_{1,3} \det \mathbf{M}_{1,3} - \cdots + (-1)^{1+n} a_{1, n} \det \mathbf{M}_{1,n}\]

Для матриці $\mathbf{A}$ розміром $2 \times 2$, наприклад,

\[\det \mathbf{A} = \det \begin{bmatrix} a_{1, 1} & a_{1, 2} \\ a_{2, 1} & a_{2, 2} \end{bmatrix} = a_{1, 1} \cdot a_{2, 2} - a_{1, 2} \cdot a_{2, 1}\]

3.2.5 Геометричний зміст матриць

Технічні визначення операцій над матрицями можуть видаватись надмірно деталізованими і неінтуїтивними правилами, котрі просто необхідно завчити. Однак, всі ці правила мають очевидний геометричний зміст, котрий рідко використовують в поясненнях базової теорії матриць 3Blue1Brown 2023.

В першу чергу, необхідно зрозуміти поняття вектора. В багатьох чисельних методах і, зокрема, в програмному середовищі R, векторами звуться скінченні ряди чисел, наприклад, змінна в наборі даних. Однак, зі шкільної програми математики можна пригадати, що векторами є і спрямовані відрізки. Наприклад, якщо позначити вектор $\vec{a}$ як $\vec{a} = (1, 2)$, то ряд чисел $(1, 2)$ можна зобразити як такий вектор, що починається з координат $(x_0 = 0, y_0 = 0)$ і закінчується координатами $(x_1 = 1, y_1 = 2)$.

Уявімо простір таких векторів. З попереднього параграфу можна помітити, що хоча й, формально, вектор має дві точки (в двовимірному просторі це $(x_0, y_0)$ та $(x_1, y_1)$), для кожного вектору одна з точок буде однаковою: $(x_0 = 0, y_0 = 0)$. Відтак, ми не втратимо ніякої інформації, якщо для багатьох векторів ми забудемо про початкові точки і визначимо лише кінцеві точки. У двовимірному просторі можна визначити скільки завгодно векторів/точок $\vec{v_1} = (x_{1, 1}, y_{1, 1}), \vec{v_2} = (x_{1, 2}, y_{1, 2}), \cdots, \vec{v_i} = (x_{1, i}, y_{1, i})$, але, звісно, це справджуватиметься і для одного виміру ($\vec{v_1} = (x_{1, 1}), \vec{v_2} = (x_{1, 2}), \cdots, \vec{v_i} = (x_{1, i})$), і для трьох вимірів ($\vec{v_1} = (x_{1, 1}, y_{1, 1}, z_{1, 1}), \vec{v_2} = (x_{1, 2}, y_{1, 2}, z_{1, 2}), \cdots, \vec{v_i} = (x_{1, i}, y_{1, i}, z_{1, i})$), і для будь-якої скінченної кількості вимірів. В структурі даних, відтак, хоча й ряди чисел є векторами, ми можемо уявити кожне спостереження як точку у просторі параметрів цього спостереження (т. зв. точка даних, або data point, що ж еквівалентним одиночному спостереженню).

Для простору векторів, матриця є лінійною трансформацією. Тобто, якщо помножити координати точки (або вектору, що є тим самим) на матрицю, то на виході ми отримаємо інший лінійний вектор. Подібно до математичної функції, ми можемо застосувати лінійну трансформацію до всього простору, і отримаємо інший простір, в котрому точки знаходяться та пропорційній до вихідного простору відстані одна від одної, а прямі між точками залишаються прямими¹⁵.

Пригадаймо правила множення матриць. Для цього потрібно кожен вектор уявити у вигляді матриці. Наприклад, для вектору \[\vec{a} = (x_1 = 1, y_1 = 2) = \begin{bmatrix} x_1 = 1 \\ y_1 = 2 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\]

застосуймо матрицю

\[\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\]

\[ \mathbf{A} \vec{a} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \end{bmatrix}= \begin{bmatrix} 1 \cdot 1 + 2 \cdot 2 \\ 1 \cdot 3 + 2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 5 \\ 11 \end{bmatrix} \]

Тобто після застосування лінійної трансформації до вектору ми отримуємо вектор такої ж розмірності, при чому ця лінійна трансформація може бути застосована для будь-якого вектору такої розмірності. Тож матриця $\mathbf{A}$ відповідає лінійній трансформації, зображеній на Рис. 3.8.

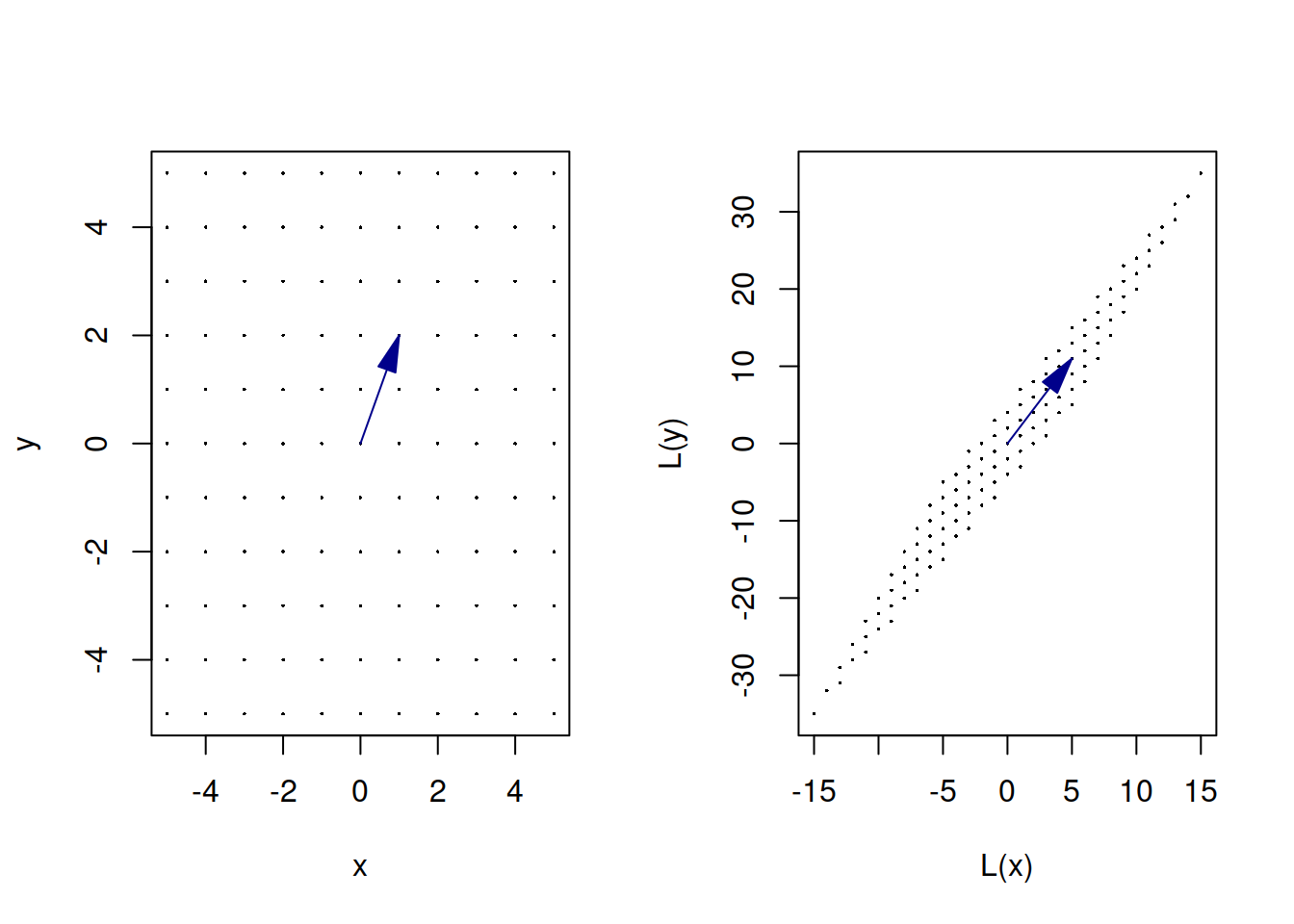
$Матриця $\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ як лінійна трансформація простору. Вектор $\vec{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}$ є лише частиною цього простору.$

Рис. 3.8: Матриця $\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ як лінійна трансформація простору. Вектор $\vec{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}$ є лише частиною цього простору.

Загалом, для всякого двовимірного простору можна уявити два незалежні базові вектори: $\hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$ й $\hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Тоді будь-який вектор $\vec{v}$ є сумою векторів, що відображають добутки певної константи $a$ та $\hat{i}$ й $b$ та $\hat{j}$: $\vec{v} = a \hat{i} + b \hat{j}$, а, відтак, всяку лінійну трансформацію $L(\cdot)$ можна виразити у вигляді \[L(\vec{v}) = a L(\hat{i}) + b L(\hat{j})\]

відтак, лінійна трансформація вектору $\begin{bmatrix} x \\ y \end{bmatrix} \rightarrow L \left( \begin{bmatrix} x \\ y \end{bmatrix} \right)$ є тотожною лінійній трансформації базових векторів, шкалованих на певні константи для базових векторів:

\[L \left( \begin{bmatrix} x \\ y \end{bmatrix} \right) = x[L (\hat{i})] + y[L(\hat{j})] = \begin{bmatrix} x L(1) & xL(0) \\ y L(0) & y L(1) \end{bmatrix}\]

Тобто сутність квадратної матриці як репрезентації лінійної трансформації – це сукупність координат, на які припадають базові вектори після лінійної трансформації. Для попереднього прикладу $\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$, зокрема, $L(\hat{i})$ матиме координати $(1, 3)$, а $L(\hat{j})$ – $(2, 4)$.

Якщо розглядати матрицю як носій інформації про лінійну трансформацію, то множення матриць є нічим іншим, як застосуванням лінійної трансформації до лінійної трансформації. Тобто, якщо уявити дві лінійні трансформації $L_1$ та $L_2$ такі що

\[L_2 \left( L_1 \left( \begin{bmatrix} x \\ y \end{bmatrix} \right) \right) = \begin{bmatrix} a & c \\ b & d \end{bmatrix} \left( \begin{bmatrix} e & g \\ f & h \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \right) = \left( \begin{bmatrix} a & c \\ b & d \end{bmatrix} \begin{bmatrix} e & g \\ f & h \end{bmatrix} \right) \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]

Із рисунку 3.8 можна помітити, що площа фігур в просторі змінюється в результаті лінійної трансформації. Детермінант матриці відображає зміну площі квадрата зі сторонами $\hat{i}$ та $\hat{j}$ таким чином, що $A[L(\hat{i} \times \hat{j})] = c \cdot A[(\hat{i} \times \hat{j})]$. Якщо $c = 0$, то матриця з таким детермінантом позначає лінійну трансформацію, що призводить до зменшення розмірності вектора, а якщо $c<0$, то (подібно до того, як від’ємна площа має сенс в інтегруванні) змінюється орієнтація $\hat{i}$ відносно $\hat{j}$.

Іншим поширеним застосуванням матриць є вирішення квадратних рівнянь. Наприклад, систему вигляду

\[\begin{cases} a_1 x + b_1 y + c_1 z = d_1 \\ a_2 x + b_2 y + c_2 z = d_2 \\ a_3 x + b_3 y + c_3 z = d_3 \end{cases}\]

можна зобразити у вигляді матриць:

\[\begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix} \iff \mathbf{A} \vec{x} = \vec{v}\]

і систему можна вирішити, якщо існує така $\mathbf{A^{-1}}$, що $(\mathbf{AA^{-1}}) \vec{w} = \vec{w}$ (тобто добуток цих двох матриць відображає таку лінійну трансформацію, яка не змінює вихідні вектори – таку трансформацію і кодує одинична матриця). Тоді $\mathbf{A^{-1} A} \vec{x} = \mathbf{A^{-1}} \vec{v}$, отже, $\vec{x} = \mathbf{A^{-1}} \vec{v}$.

Очевидно, ці дві умови не завжди можуть справджуватися, у випадку чого трансформація не є лінійною.↩︎