4.8 Моделювання популяцій
В попередніх розділах ми розглянули концептуальні моделі динаміки популяції та метапопуляції. Як би і пасувало екології, ці моделі не обмежуються туманними визначеннями й беззмістовними діаграмами65, а ґрунтуються на конкретному й формально визначеному математичному апараті. Втім, навіть цей математичний апарат є лише концепцією, і описує абстрактну популяцію абстрактного виду. Теорії динаміки популяцій та метапопуляцій може наштовхнути на якісні висновки (наприклад, як-то теорія метапопуляцій передбачає позитивний ефект збільшення з’єднаності між локальними популяціями на виживання метапопуляції), однак їх досі важко застосовувати до реальних систем66.
В цьому розділі ми оглянемо більш прикладні моделі, котрі можна використати для опису динаміки реальних популяцій та – що особливо важливо для охорони природи – їх зміни в майбутньому. Перед тим, як читати цю секцію, варто пригадати різні математичні трюки: наприклад, оцінку параметрів через функцію максимальної правдоподібності та правила множення матриць. В цьому розділі читач знайде секції про:
моделі на базі диференційних рівнянь із особливими випадками (варто почитати для загального розвитку),
матричні моделі для опису динаміки демографічної структури популяції,
агентні моделі, що можуть симулювати кожну окрему особину в популяції.
Варто також згадати, що під “моделюванням популяцій” хтось також може мати на увазі просторове моделювання поширення видів (species distribution models, SDMs). Справді, існують способи перебачити ймовірність присутності видів на географічних локаціях, однак ці методи ґрунтуються на понятті екологічної ніші, тож в цьому розділі ми їх не розглядатимемо.
4.8.1 Диференційні моделі
Усі розглянуті вище моделі є прикладами диференційних або різницевих рівнянь: всі вони описують зміну певного параметру (чисельності популяції, кількості заселених локацій тощо) із іншим параметром – часом67. Диференційні рівняння є дуже потужним інструментом, яким послуговуються численні дисципліни, і, відтак, існують розроблені методи й алгоритми для роботи з ними на кшталт пакету deSolve для R. З іншого боку ж, до диференційних моделей варто ставитись із обережністю, адже вони є лише математичною репрезентацією, котра нічого не знає про біологічні процеси. Наприклад, уявімо просту дискретну модель експоненційного росту вигляду \(N_\tau = N_{\tau-1} + r N_{\tau-1}\) із параметром \(r = 0.25\). Скажімо, в початковому стані системи ми мали 10 особин в популяції, \(N_0 = 10\), тоді на наступному кроці ми матимемо \(N_1 = N_0 + rN_0 = 10+0.25\cdot10 = 12.5\). З біологічної точки зору, що таке 12.5 особин? Кількість особин може бути тільки дискетною змінною, це або 12, або 13 особин. Може, просто заокруглити значення? Ні, в такому випадку модель видаватиме хибні значення із похибкою, що тільки збільшується з часом. Популяційному біологу залишається лише ігнорувати таку неточність моделі.
Подібним чином, диференційні рівняння можуть генерувати негативні значення, що не є чимось незвичним з математичної точки зору, але є абсурдним з біологічної. Застосування диференційних рівнянь може вводити нереалістичні припущення моделей: наприклад, в класичній теорії метапопуляцій параметр \(p\) — частка заселених локацій в системі — може приймати будь-яке значення між нулем та одиницею. Це передбачає, що в системі існує безкінечна кількість локацій, адже інакше \(p\) б мало певну роздільну здатність68. Втім, знову ж, навіть з такими недоліками диференційні рівняння є потужним методом, і тому є дуже поширеними в сучасній екології. Нижче я хочу навести декілька прикладів використання диференційних моделей в реальних системах.
4.8.1.1 Форма щільність-залежної регуляції
Раніше ми вже згадували тета-логістичний ріст. Пригадайте, що в загальному вигляді тета-логістичний ріст має вигляд
\[\frac{dN}{d\tau} = rN \left( 1 - \left( \frac{N}{K} \right)^\theta \right)\]
де \(\theta\) описує залежність між темпами росту популяції та її щільністю, або, іншими словами, наскільки регуляція росту популяції є щільність-залежною або -незалежною. Якщо
\(\theta = 1\), модель описує простий логістичний ріст із лінійною залежністю від чисельності;
\(\theta < 1\), модель описує увігнутий зв’язок (Рис. 4.14): це притаманно для видів, котрі мають щільність набагато нижчу за ємність середовища і піддаються ефектам середовища навіть за низької щільності;
\(\theta > 1\), модель описує випуклий зв’язок: великі, довгоживучі організми, популяції котрих близькі до ємності середовища, і лімітовані доступністю ресурсів; такі популяції не надто піддаються ефектам середовищам аж допоки вони не наблизяться до ємності середовища; за низької ж щільності, щільність-залежна регуляція, ефективно, відсутня.
).](bookdown-demo_files/figure-html/fig-theta-pgr-1.png)
Рис. 4.14: Зв’язок між щільністю популяції та темпами її росту за різних значень параметру \(\theta\) за тета-логістичного росту із параметрами \(r = 0.1, K = 100\) (за Sibly et al. 2005).
У своїй знаковій роботі, Сіблі та співавтори (2005) проаналізували більш ніж 3 тисячі довгострокових часових серій, що описували чисельність популяцій 674 видів комах, кісткових риб, птахів, та ссавців. Для кожної часової серії, покрокові значення щільності популяції \(N_{\tau}\) дозволили оцінити темп росту популяції як \(y = \ln(\frac{N_{\tau}}{N_{\tau - 1}})\). Далі, автори взяли набір потенційних значень \(\theta\) в діапазоні \((-10^{1.5}, 10^{1.5})\), і для кожного потенційного значення побудували нелінійну69 регресію вигляду \(y = \beta_0 + \beta_1 N^{\theta}\). Таке значення \(\theta\), яке видавало наймешу суму квадратів залишків, визначали як шукане \(\hat{\theta}\) для цієї популяції.
Для переважної більшості аналізованих популяцій, оцінка \(\theta\) була меншою за одиницю, тобто більшість проаналізованих видів відчувають ефекти щільність-залежної регуляції навіть за низької щільності популяції. Оскільки функція темпу росту від щільності популяції за \(\theta < 1\) не надто змінюється коли \(N \rightarrow K\) (Рис. 4.14), це також означає що популяції можуть витрачати значний час поблизу ємності середовища або навіть його перевищувати. Для природоохоронців цей резуьтат також означає, що припущення про лінійну щільність-залежну регуляцію (класичний логістичний ріст) із доступними, скажімо, з літературних джерел, оцінками \(r\) та \(K\) є доволі небезпечними, адже якщо популяція насправді виявляє \(\theta < 1\), то швидкість її відновлення буде набагато повільнішою, аніж передбачення за \(\theta = 1\).
4.8.1.2 Пошук детермінантів росту популяції
Отже, існують докази щільність-залежної регуляції темпу росту популяцій багатьох видів. Які ж механізми впливу щільності популяції на її темпи росту? Сіблі та Хон (2003) запропонували три основні підходи до визначення детермінантів \(r\):
щільнісна парадигма (density paradigm) передбачає, що щільність-залежна регуляція оперує через смертність, виживання, та продуктивність популяцій; в цьому контексті варто згадати аналіз k-значень (k-value analyses), котрий намагається оцінити так званий “вбивчий потенціал” середовища (killing power) оцінений як частка популяції, втрачена протягом певного часового проміжку;
демографічна парадигма (demographic paradigm) фокусується на зв’язку між темпами росту популяції та вікової структури популяції, постулючи що кожна вікова група в популяції матиме різні темпи смертності та народжуваності; наприклад, серед видів-довгожителів, ефект смертності/виживання переважає над ефектом темпів розмноження, в той час як види із короткою тривалістю життя мають швидко розмножуватись;
механістична парадигма (mechanistic paradigm), головним чином, намагається передбачити темпи росту популяції як функцію від зовнішніх факторів, наприклад, клімату, доступності кормів, хижаків тощо.
Хон та Сіблі (2003) продемонстрували застосування цих парадигм на прикладі наборів даних щодо чисельності сипухи (Tyto alba) і її корму, полівок Taylor 1994. Ці автори намагались підлаштувати базову модель вигляду \(N_{\tau + 1} = N_{\tau} \cdot \exp[a + bN_{\tau} + cv]\) (де \(v\) – наявність корму, \(\{a, b, c\}\) – коефіцієнти) до цього набору даних із наступними варіаціями:
дискретний експоненційний ріст \(N_{\tau + 1} = N_{\tau} \lambda^{\tau} = N_{\tau} \exp[r\tau]\) (нульова модель)
логістичний ріст із коефіцієнтом \(c = 0\), тобто \(N_{\tau + 1} = N_{\tau} \cdot \exp[a + bN_{\tau}]\) (щільнісна парадигма)
функція за типом Соломона (Solomon-type), де розмір популяції визначається доступністю корму (тут – регресія між розміром популяції сов та щільністю популяції полівок) (механістична парадигма)
функція за типом Кохлі (Caughley-type), що визначає ефект щільності популяції через конкуренцію за ресурс, наприклад, прирівнянням коефіцієнту \(b = 0\): \(N_{\tau + 1} = N_{\tau} \cdot \exp[a + cv]\) (механістична парадигма)
модель Денніса-Оттен, що включає ефекти наявності корму і щільності популяції фокального виду (тобто \(b \neq 0\), \(c \neq 0\)) (механістична парадигма)
двостадійна модель Ейлера-Лотки \(\lambda ^{\alpha} (1 - \frac{s}{\lambda}) = lb\) де \(\alpha\) – мінімальний репродуктивний вік, \(s\) – виживання дорослих особин протягом року, \(l\) – виживання між народженням до репродуктивного віку, \(b\) – річна продуктивність (самиць на дорослу самицю) (демографічна парадигма).
Автори описують покрокову оцінку параметрів моделі: (1) темпи росту популяції \(\lambda\) як частку гніздових пар, котрі успішно розмножувались в певний рік; (2) внутрішній темп росту \(r\) через регресію приросту популяції (\(\ln[N_{\tau + 1}/N_{\tau}]\)) на чисельність популяції (\(N\)), в якій інтерсепт із вертикальною віссю відповідає внутрішньому темпу росту (\(r\) – такий темп росту, коли чисельність популяції нульова), а із горизонтальною – ємності середовища (\(K\)); (3) функцію за типом Соломона як лінійну регресію чисельності популяції сов на щільність популяції полівок, та функцію за типом Кохлі через лінійну регресію \(r\) на щільність популяції полівок; (4) демографічні параметри (\(\alpha, s, l, b\)) – через польові спостереження. Із цих моделей, найбільш інформативною видалась повна функція за типом Кохлі, котра включала ефекти щільності фокальної популяції сов та щільності популяції полівок.
Демографічну парадигму можна розвинути далі через введення щільність-залежних моделей із віковою структурою та авторегресійною динамікою70 (Lande et al. 2002, Lande et al. 2003). Так, просту модель вигляду \(N_{\tau} = N_{\tau - 1} \cdot \lambda N_{\tau -1}\), якщо припустити, що вона коливається навколо точки рівноваги, можна розвинути до складнішого випадку, котрий включає вікову структуру популяції:
\[N_{\tau} = N_{\tau - 1} \times s(N, \tau - 1) \times \phi (N, \tau - \alpha, \cdots, \tau - 1)\]
де функція \(s(\cdot)\) визначає ймовірність виживання дорослих особин протягом року і визначається як
\[s(N, t) = \bar{s} (N_t) + \zeta(t)\]
де \(\bar{s}(N_t)\) – середнє виживання популяції дорослих особин протягом року в популяції розміру \(N_t\) і \(\zeta(t)\) відповідає ефекту випадкових пертурбацій середовища, а функція \(\phi(\cdot)\) визначає приріст дорослих особин як добуток щорічного репродуктивного потенціалу популяції (продукція самиць на дорослу самицю) та виживання особин протягом першого року життя:
\[\phi(N, t - \alpha, \cdots, t - 1) = f(N, t - \alpha) \times \prod \limits_{i=1}^{\alpha - 1} s_{\alpha - i} (N, t-i)\]
де \(f(N, t) = \bar{f}(N_t) + \epsilon(t)\) визначає щорічну продуктивність самиць із врахуванням пертурбацій \(\epsilon\), та \(s_x(N, t) = \bar{s}(N_t) + \delta(t)\) визначає ймовірності річного виживання між віком \(i\) та \(i + 1\) для \(1 \leq x \leq (\alpha - 1)\).
В цілому, така модель може видаватись дуже страшною, але вона дозволяє ввести літературні дані щодо історії життя видів (наприклад, продуктивність самиць, річне виживання особин, особливості вікової структури популяцій) та стохастичність середовища (\(\zeta, \epsilon, \delta\)) в диференційні моделі із подальшою можливістю оцінки щільність-залежності в динаміці популяцій. Математично, така модель також дозволяє оцінити сумарний ефект смертності дорослих особин й щільність-залежності через суму коефіцієнтів авторегресії в системі (Lande et al. 2003).
4.8.1.3 Врахування стохастичності середовища
В природних системах, темпи росту популяції регулються як щільність-залежними механізмами, так і щільність-незалежними. У рандомному середовищі суто щільність-незалежний ріст можна уявити як \(N_{\tau + 1} = N_{\tau} \times \lambda_{\tau}\), де \(\lambda_{\tau}\) є темпом росту і є випадковою змінною, \(\lambda_{\tau} \sim \mathcal{N}(\bar{\lambda}, \sigma_{\lambda}^2)\) (Рис. 4.15, Sæther & Engen 2003).
Code
sigma_l <- 0.3
t <- 1:250
pop <- lapply(1:5, function(x) c(log(20), numeric(249)))
for (j in 1:5){
for (i in 2:250){
dn <- rnorm(1, 0.06, sigma_l)
# dn <- exp(dn)
dn <- ifelse(dn < -(pop[[j]][i-1]), 0, dn)
pop[[j]][i] <- pop[[j]][i-1] + dn
}
}
pop <- lapply(pop, exp)
plot(x = t, y = pop[[1]], type = "l", log = "y",
ylim = c(1, max(unlist(pop))), col = "darkgray",
xlab = "Час, τ", ylab = "Чисельність популяції, N")
lines(x = t, y = pop[[2]], col = "darkgray")
lines(x = t, y = pop[[3]], col = "darkgray")
lines(x = t, y = pop[[4]], col = "darkgray")
lines(x = t, y = pop[[5]], col = "darkgray")
lines(x = c(1, 250), y = c((20), exp(17.935732)))).](bookdown-demo_files/figure-html/fig-random-growth-1.png)
Рис. 4.15: П’ять симуляцій щільність-незалежного росту із стохастичним темпом росту \(\log(\lambda_{\tau})\), чорна лінія відповідає траекторії росту популяції без стохастичних ефектів (за Sæther & Engen 2003).
Якщо ігнорувати демографічну стохастичність, то стохастичність середовища (\(\sigma_e^2\)) прямо впливає на варіацію темпів росту: \(\sigma_{\lambda}^2 = \sigma_e^2\). Якщо перевести розміри популяцій на лог-шкалу, то \(X_{\tau} = \ln(N_{\tau})\), \(r_{\tau} = \ln(\lambda_{\tau})\), і модель набуває вигляду \(X_{\tau + 1} = X_{\tau} + r_{\tau}\). Для такої системи, середній ріст популяції протягом проміжку часу \(t\) можна оцінити як \(s = \mathbb{E}[r]\), а його варіацію – як \((\sigma_{\lambda}^2)/t\). Якщо ж ввести демографічну стохастичність, \(\sigma_d^2\), то стохастичний темп росту становитиме \(s \approx \ln(\bar{\lambda}) - \frac{\sigma_e^2}{2} - \frac{\sigma_d^2}{2N}\): тобто за малої чисельності популяції, демографічна стохастичність вносить детерміністичне зменшення довгострокового темпу росту популяції. Для великих популяцій (таких, що \(N \gg \sigma_d^2/\sigma_e^2\)) стохастичність середовища має більший вклад до темпу росту популяції, аніж демографічна стохастичність.
За щільність-залежного сценарію, темп росту популяції за певного розміру популяції складає \(r(N) = \mathbb{E}[(\lambda-1)|N]\), і ефект щільність-залежності можна описати через рівняння тета-логістичного росту:
\[\mathbb{E} \left[ \frac{\Delta N}{N} | N\right] = r \left[ 1 - \left( \frac{N}{K} \right)^{\theta} \right]\]
В такій системі, нестабільність динаміки популяції зменшується зі збільшенням параметру \(\theta\), адже цей параметр прямо пов’язаний зі швидкістю повернення популяції до рівноваги після збурення (тобто, із характерним темпом повернення). Для тета-логістичного росту можливо аналітично знайти рівноважний розподіл чисельності популяції (Sæther & Engen 2003) як:
\[\frac{K^2 \mathcal{\Gamma} (\frac{\alpha + 2}{\theta})}{[\frac{\alpha + 1}{\theta}]^{2/\theta} \times \mathcal{\Gamma}(\frac{\alpha}{\theta})}\]
де \(\mathcal{\Gamma}(\cdot)\) є гамма-функцією \(\mathcal{\Gamma}(x) = \int \limits_0^{\infty} t^{x-1} \exp[-t] dt\), а \(\alpha = 2r(1)/\sigma_e^2(1 - K^{-\theta}) - 1\), де \(r(1)\) – це темп росту популяції, коли її чисельність становить \(N=1\).
Загалом, мабуть, знати точну формулу стаціонарного розподілу ймовірності для рівноважного розміру популяції за стохастичного середовища та демографії не дуже треба, але варто розуміти, що вона означає: всі ці кроки в розрахунках показують нам, що якщо уявити темпи росту популяції та демографічні процеси не як точкові оцінки, а як розподіли із певною варіацією, то й динаміка популяції матиме певну невизначеність (і, отже, й матиме якийсь розподіл густини ймовірності). Якщо на руках є модель популяції із включеною невизначеністю, тоді можна, наприклад, аналітично оцінити ймовірність вимирання цієї популяції за різних сценаріїв збурень середовища (які можна позначити через збільшення стохастичності середовища \(\sigma_e^2\)).
Така модель також передбачає, що за низьких значень \(\theta\) варіація темпу росту \(r\) матиме значний вплив на стаціонарний розподіл популяції. Варто також помітити, що стаціонарний розподіл популяції не включає ефекту демографічної стохастичності: якщо \(\sigma_d^2 > 0\), то система не досягає стаціонарного стану. Це означає, що ігнорування демографічної стохастичності може викликати значну похибку в оцінках ймовірності вимирання чи часу до вимирання популяції (Sæther & Engen 2002).
4.8.1.4 Врахування помилок обліків
Оцінка параметрів росту популяції вимагає точних наборів даних із часовими серіями розмірів популяції чи їх щільності. Що якщо існує певна невизначеність в оцінці щільності популяції? Наприклад, якщо дані походять із багатьох спостережників, кожен із яких може іноді неправильно визначити вид або не помітити особину виду. Для таких випадків, звісно, можна написати ще складнішу модель (Dennis et al. 2006).
В процесі отримання даних про чисельність популяції варто розрізняти два дуже різних джерела варіації. По-перше, чисельність популяції ніколи не буде точно дорівнювати значенням, які видає математична модель. Модель за визначенням є ідеалізованою, а в реальних системах завжди присутній статистичний шум, який також можна назвати шумом процесу (process noise). По-друге, неточність в даних може походити із процесу спостереження, що можна позначити похибкою спостереження (observation error). В контексті популяційної динаміки, для врахування шуму процесу та похибки спостереження можна почати із базової моделі простору станів Ґомпертца (Gompertz state-space model, GSS):
\[N_{\tau} = N_{\tau-1} \times \exp[a + b + \ln(N_{\tau-1}) + \epsilon_{\tau}]\]
де \(\{a, b\}\) є параметрами, \(\epsilon_{\tau}\) – таким випадковим шумом процесу, що \(\epsilon_{\tau} \sim \mathcal{N}(0, \sigma^2)\). На лог-шкалі, GSS є авторегресійним процесом першого порядку (\(\text{AR}(1)\)): якщо прийняти \(X_{\tau} = \ln(N_{\tau})\):
\[X_{\tau} = X_{\tau - 1} + a + b X_{\tau - 1} + \epsilon_{\tau} \stackrel{c = (1+b)}{=} a + c X_{\tau - 1} + \epsilon_{\tau}\]
Ми ніколи не можемо точно оцінити \(X_{\tau}\) через похибку спостереження. Відтак, позначимо результати спостереження як \(Y_{\tau} = X_{\tau} + F_{\tau}\) де \(F_{\tau}\) є такою помилкою спостереження, що \(F_{\tau} \sim \mathcal{N}(0, \xi^2)\). Тоді можна отримати повну модель із детерміністичною та стохастичною частинами:
\[Y_{\tau} = \color{darkgreen}{a + cY_{\tau-1}} + \color{darkred}{(\epsilon_{\tau} + F_{\tau} - cF_{\tau-1})}\]
\(Y_{\tau}\) є прикладом не-Марківського71 ARMA72 процесу. В цій моделі параметри \(\{a, c, \sigma^2, \xi^2\}\) можна оцінити а допомогою алгоритмів пошуку максимальної правдоподібності або обмеженої максимальної правдоподібності73. Денніз та ін. (2006) попереджають, втім, що функції правдоподібності можуть мати декілька локальних атракторів, тому особливо важливо проводити пошук максимальної правдоподібності в якнайширшому діапазоні параметрів. Таке завдання може вимагати тривалих комп’ютерних обчислень.
Модель із врахуванням шуму процесу та похибки спостереження може мати наступні особливі випадки:
коли “під капотом” процесу \(X_{\tau}\) є суто детерміністичним, тобто \(\sigma^2 = 0\);
коли спостереження є абсолютно точними (\(\xi^2 = 0\)), модель описує тільки шум процесу;
щільність-залежність можна вимкнути, якщо прийняти \(c = 1 \Leftrightarrow b = 0\), і тоді модель описує стохастичний експоненційний ріст із похибкою спостереження, що можна використати як нульову модель в аналізі життєздатності популяції.
В стохастичних моделях, поняття ємності середовища \(K\) стає зайвим і надмірним, адже стаціонарний розподіл рівноважного розміру популяції відображає очікування довгострокового стану популяції, навколо якого трапляються флуктуації. Популяція в рівноважному стані буде 95% часу буде перебувати в межах 95-ти перцентилів стаціонарного розподілу, що можна використати для моделювання стохастичності реальних популяцій та оцінки ймовірності їх вимирання.
4.8.1.5 Внутрішньовидова негативна щільність-залежна регуляція
Похідні моделей динаміки популяції можна включати в дослідження складніших екологічних питань. Наприклад, який внесок щільність-залежної регуляції в підтримку рівнів біорізноманіття? Коли говорити про біорізноманіття, це передбачає існування більш ніж одного виду в системі, тому можна виділити
внутрішньовидову щільність-залежність (conspecific negative density dependence, CNDD), котра сповільнює темпи росту популяції за її високої чисельності через, наприклад, природних ворогів чи конкуренцію за обмежений ресурс (що має стабіліізуючий вплив на розвиток популяції), та
міжвидову щільність-залежність (heterospecific megative density dependence, HNDD), котра впливає на всі види в системі однаково через міжвидові взаємодії чи хижаків-генералістів; за цього механізму, збільшення розміру однієї популяції заповільнює темпи росту всіх популяцій в системі.
Врахувати ці два механізми можна на базі моделі Рікера:
\[N_{\tau + 1} = N_{\tau} \times \exp \left[ r \times \left(1 - \frac{N_{\tau}}{K} \right) \right]\]
із врахуванням CNDD та HNDD (LaManna et al. 2017), що визначає чисельність виду на локації як випадкову змінну \(N_i \sim \mathcal{NegBin}(\hat{N_i}, \gamma)\), де
\[\hat{N_i} = N_{ad} \times \exp \left[ r + \text{CNDD} \cdot N_{ad} + \text{HNDD}_{ad} \cdot n_{ad} + \text{HNDD}_{juv} \cdot n_{juv} \right]\]
де \(N_{ad}\) – кількість дорослих особин фокального виду, \(n_{ad}\) – кількість дорослих особин інших видів, \(n_{juv}\) – кількість молодих особин інших видів, \(\text{CNDD}\) – коефіцієнт внутрішньовидової щільність-залежності, \(\text{HNDD}_{ad}\) – міжвидова щільність-залежність між дорослими особинами, \(\text{HNDD}_{juv}\) – міжвидова щільність-залежність між молодими особинами.
ЛаМанна та співатори (2017) оцінили інтенсивність CNDD та HNDD в 24 лісових системах на різних континентах. Цікаво, що, хоча й модель Рікера описує динамічну систему, модифікація моделі використана тут не потребує даних часових серій, адже параметризація моделі відбувається на даних щодо чисельності дорослих та молодих дерев на локації в один момент часу. В глобальному масштабі, ефект CNDD для рідкісних видів збільшується ближче до тропічних екосистем. Оскільки CNDD має ефект стабілізації на динаміку популяції, збільшення ролі CNDD порівняно із HNDD може надати пояснення підтримці рівнів біорізноманіття в екосистемах із високим різноманіттям. Втім, із подібними механізмами ми ознайомимося пізніше (наприклад, із гіпотезою Джензена-Конела), а на цьому моменті нас має хвилювати лише елегантність модифікації диференційної моделі Рікера.
4.8.2 Матричні моделі
“Навіщо нам взагалі вчити матриці?”
— типові студенти біологічного факультету
Цей день настав. Нарешті, ми закінчили обговорювати різні заплутані диференційні рівняння, і тепер час відповісти на одвічне питання студентів-біологів на курсах основ вищої математики – яка користь від множення матриць в біології? Насправді, цей нескладний метод використовувався в популяційній біології дуже тривалий час (Leslie 1945), і я пропоную розглянути цей підхід на прикладі.
Хто не любить морських черепах? Ви, мабуть, бачили принаймні один документальний фільм про те, як доросла морська черепаха вилазить на берег океану, будує гніздо, із якого невдовзі вилуплюються мініатюрні черепашата, котрі з усіх сил намагаються перебігти через пляж, перебороти хвилі, і, врешті, пірнути у воду, і в процесі при тому намагаються не бути впольованими різноманітними хижаками. Не дивно, що такий сентимент викликає чимало інтересу серед волонтерів, що мчать стерегти гнізда черепах від браконьєрів й хижаків. Але що можна підглянути з точки зору наукового підходу популяційної біології замість сентиментальної охорони природи?
Візьмемо до прикладу довгоголову морську черепаху (Caretta caretta). Уявімо популяцію, що складається із трьох стадій: яйця, молоді особини, й дорослі особини. Тільки дорослі особини можуть розмножуватись, і кожна стадія має певний рівень виживання. Задля спрощення, приймемо, що один крок часу дорівнює одному року. Скажімо, кожна доросла самиця відкладає 60 яєць; кожне яйце вилупляється, але тільки 10% черепашенят доживає до статусу молодої особини. Молоді ж особини ж мають 40% дожити до репродуктивного віку і розмножитись (припускаючи 1:1 пропорцію самців і самиць, продукція, в середньому, складатиме 30 яєць на дорослу особину). В принципі, таку систему можна описати системою різницевих рівнянь: якщо прийняти, що \(n_0\) – це чисельність яєць в популяції, \(n_{juv}\) – чисельність молодняка, \(n_{ad}\) – чисельність дорослих особин, \(s_0 = 0.1\) – ймовірність яйця вилупитись і успішно вижити до стадії молодої особини, \(s_{juv} = 0.4\) – ймовірність для молодої особини дожити до статевої зрілості, \(f_{ad} = 30\) – репродуктивний потенціал дорослої особини, то динаміку такої структурованої популяції можна описати як
\[ \begin{cases} n_{0, \tau} = f_{ad} \times n_{ad, \tau - 1} \\ n_{juv, \tau} = s_0 \times n_{0, \tau-1} \\ n_{ad, \tau} = s_{juv} \times n_{juv, \tau-1} \end{cases} \]
З такою системою рівнянь, може, і можна працювати, але це може бути доволі незручним, вимагати тривалого часу на обчислення, і за складнішої структури популяції стає легше припуститись помилки в рівняннях. Тут в пригоді може стати матриця: ймовірності виживання до наступної стадії і продуктивність особин мають дуже подібний зміст до ймовірності переходів в ланцюгах Маркова. Тож динаміку популяції можна зобразити як матрицю:
\[ \textbf{L} = \begin{bmatrix} \color{gray}{0} & \color{gray}{0} & f_{ad} \\ s_0 & \color{gray}{0} & \color{gray}{0} \\ \color{gray}{0} & s_{juv} & \color{gray}{0} \\ \end{bmatrix} = \begin{bmatrix} \color{gray}{0} & \color{gray}{0} & 30 \\ 0.1 & \color{gray}{0} & \color{gray}{0} \\ \color{gray}{0} & 0.4 & \color{gray}{0} \\ \end{bmatrix} \]
Якщо взяти вектор, що репрезентує вікову структуру вихідної популяції, скажімо, \(\mathbf{N}_{\tau = 0} = \{n_{0, 0} = 10, n_{juv, 0} = 5, n_{ad, 0} = 1 \}\) і перемножити його із матрицею \(\mathbf{L}\) (пам’ятаймо, що в множенні матриць їх порядок має значення, \(\mathbf{N} \times \mathbf{L}\) не дорівнює \(\mathbf{L} \times \mathbf{N}\)), то продукт цієї операції описуватиме вікову структуру популяції на наступному кроці часу (\(\mathbf{N}_{\tau = 1} = \{n_{0, 1} = n_{ad, 0}\times f_{ad}, n_{juv, 1} = n_{0, 0} \times s_0, n_{ad, 1} = n_{juv, 0} \times s_{juv}\}\)). Повторення цієї операції знову і знову дасть змогу побудувати динамічну модель популяції протягом тривалого часу:
\[ \mathbf{N}_{\tau} = \mathbf{L} \times \mathbf{N}_{\tau-1} = \begin{bmatrix} \color{gray}{0} & \color{gray}{0} & f_{ad} \\ s_0 & \color{gray}{0} & \color{gray}{0} \\ \color{gray}{0} & s_{juv} & \color{gray}{0} \\ \end{bmatrix} \times \begin{bmatrix} n_{0, \tau-1} \\ n_{juv, \tau-1} \\ n_{ad, \tau-1} \end{bmatrix} \]
Погляньмо на симуляцію такої популяції протягом п’ятидесяти часових кроків (Рис. 4.16).
Code
L = matrix(
c(0, 0, 30,
0.1, 0, 0,
0, 0.4, 0),
3, 3, byrow = T)
N <- vector("list", 50)
N[[1]] <- matrix(c(10, 5, 1), nrow = 3, ncol = 1)
for (i in 2:50){
N[[i]] <- L %*% N[[i-1]]
}
N <- do.call(cbind, N)
plot(x = 1:50, y = N[1,], type = "l",
xlab = "Час, τ", ylab = "Чисельність вікового класу")
lines(x = 1:50, y = N[2,], lty = 2)
lines(x = 1:50, y = N[3,], lty = 3)
legend("topleft", lty = 1:3, legend = c("Яйця", "Молоді особини", "Дорослі особини"))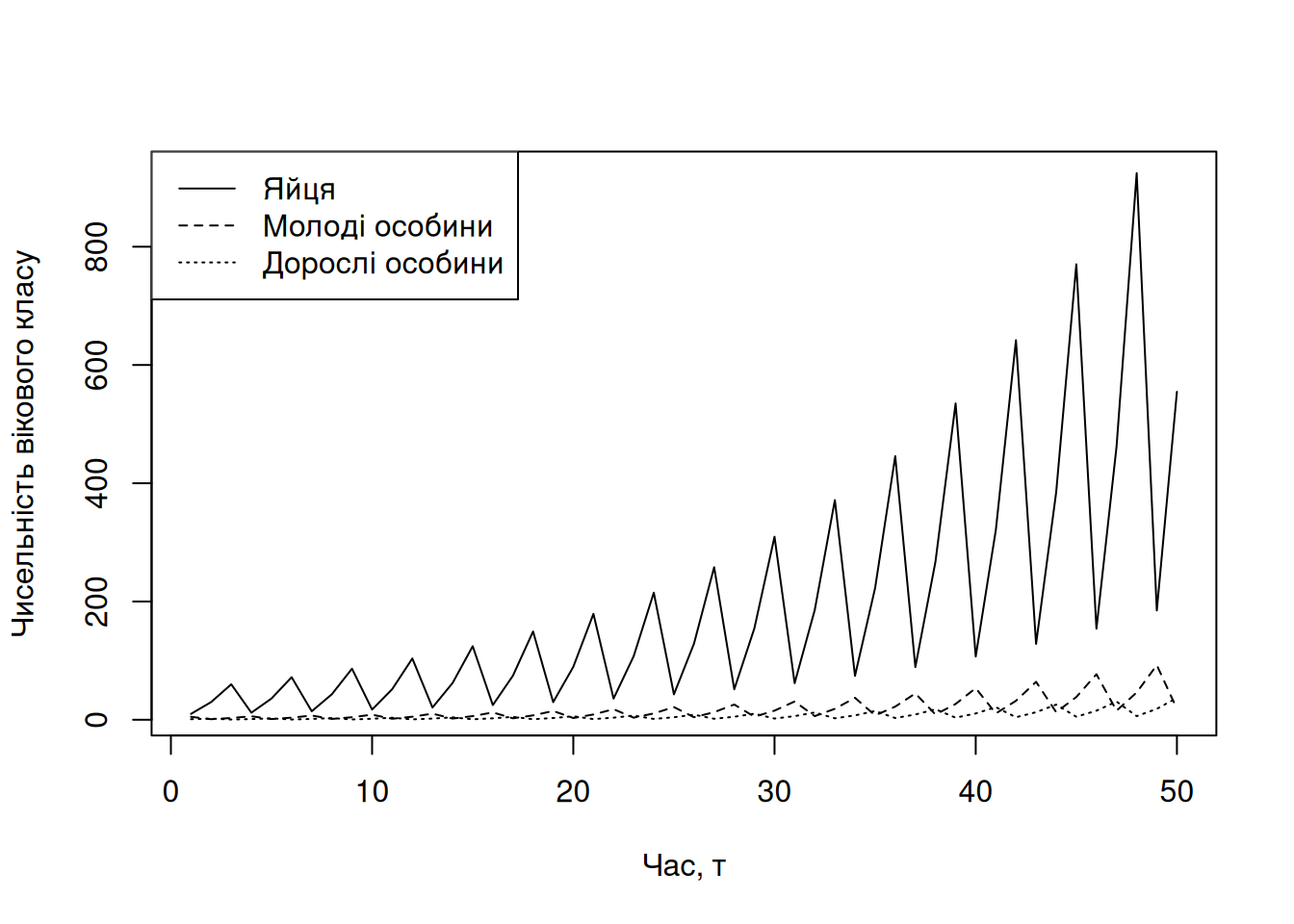
Рис. 4.16: Приклад простої симуляції динаміки популяції із віковою структурою через матрицю Леслі.
Матрицю \(\mathbf{L}\) називають матрицею Леслі (Leslie matrix). В загальному випадку, якщо в популяції із \(\alpha\) віковими класами позначити \(n_i\) як чисельність особин вікового класу \(i\), \(p_i\) – як ймовірність особини вижити один крок часу і залишитись на стадії \(i\), \(g_i\) – як ймовірність особини вижити і перейти на наступну стадію \((i+1)\), та \(f_i\) – як середній розмір потомства від однієї особини на стадії \(i\), то матриця Леслі розміру \([\alpha \times \alpha]\) матиме вигляд
\[ \mathbf{L} = \begin{bmatrix} p_1 & f_2 & f_3 & \cdots & f_{\alpha - 1} & f_{\alpha} \\ g_1 & p_2 & \color{gray}{0} & \cdots & \color{gray}{0} & \color{gray}{0} \\ \color{gray}{0} & g_2 & p_2 & \cdots & \color{gray}{0} & \color{gray}{0} \\ \color{gray}{0} & \color{gray}{0} & g_2 & \cdots & \color{gray}{0} & \color{gray}{0} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & \cdots & g_{\alpha - 1} & p_{\alpha} \end{bmatrix} \]
В багатьох випадках особини не затримуються на одній стадії, а із кожним кроком часом або помирають, або переходять на наступну стадію. В таких випадках, \(p_i=0 \text{ }\forall \text{ } i\). Багаторазове перемноження матриці Леслі \(\mathbf{L}\) на матрицю \(\mathbf{N}_{\tau}\) розміром \([\alpha \times 1]\) симулюватиме динаміку просторової популяції в часі:
\[\mathbf{N}_{\tau} = \mathbf{L} \times \mathbf{N}_{\tau-1}\]
Структуру популяції на будь-якому кроці часу \(t\) можна знайти як
\[\mathbf{N}_{\tau = t} = \mathbf{L}^{t} \times \mathbf{N}_{\tau=0}\]
Чого ж корисного можна отримати з такої моделі? По-перше, якщо знайти власні значення матриці \(\mathbf{L}\), то домінантне (найбіль позитивне) власне значення (dominant eigenvalue), яке можна позначити як \(\lambda\), відповідатиме сумарному довготерміновому темпу росту популяції. Отже, навіть без моделювання із \(\mathbf{L}\) можна зробити висновок, що розмір популяції зростає в часі (\(\lambda > 1\)), або, навпаки, зменшується (\(\lambda < 1\)). Варто відмітити, що моделі Леслі поводяться як експоненційні диференційні моделі із безкічнечним ростом або кінцевим вимиранням популяції. Як би то не було, власний вектор (eigenvector) \(\vec{w}\), що відповідає \(\lambda\), описує стаціонарний розподіл популяції за віковими групами. Цей розподіл можна використати для оцінки такої вікової структури популяції, за якої вона буде найбільш стабільною. На практиці, знайти домінантне власне значення і відповідний власний вектор можна, якщо перемножити матрицю Леслі на вихідну популяцію стільки разів, що в кожному наступному кроці всі вікові групи пропорційні до попереднього кроку на однакову константу – ця константа і є ваша \(\lambda\), а перерахунок структури популяції на частки (так, щоб сума складала одиницю) відповідатиме її власному вектору.
По-друге, коли на руках є параметризована модель Леслі, то ніщо не заважає внести зміни в різні елементи матриці (\(p_i\), \(g_i\), чи \(f_i\)), і спостерігати як це відображатиметься на темпах росту популяції \(\lambda\). Цей підхід називають аналізом чутливості (senstivity analysis), і його процедура дуже проста: збільшість чи зменшіть певний коефіцієнт в матриці Леслі на якусь фіксовану частку (наприклад, на 50%), перерахуйте власне значення \(\lambda\) нової матриці, і порівняйте з базовим \(\lambda\).
На додачу до аналізу чутливості, існує також і аналіз еластичності (elasticity analysis). Цей підхід трошки складніший, і він описує пропорційну зміну \(\lambda\) у відповідь на пропорційну зміну параметра матриці Леслі (Crouse et al. 1987). Для стаціонарної вікової структури популяції \(\vec{w}\) і власного вектору \(\vec{v}\) транспонованої матриці \(\mathbf{L}^T\), еластичність відносно параметру \(a_{i,j}\) можна обчислити як
\[\frac{\partial \ln(\lambda)}{\partial \ln(a_{i,j})} = \frac{a_{i, j}}{\lambda} \cdot \frac{\partial \lambda}{\partial a_{i, j}} = \frac{a_{i, j}}{\lambda} \left( \frac{\vec{v}_i \cdot \vec{w}_j}{\vec{v} \cdot \vec{w}} \right)\]
де \(\vec{v} \cdot \vec{w}\) є скалярним добутком цих двох векторів (\(\vec{v} \cdot \vec{w} = \sum_i \vec{v}_i \cdot \vec{w}_i\)). Якщо такі обчислення видаються занадто складними, то еластичність також можна апроксимувати за рахунок введення невеличких відхилень (скажімо, 1%) в параметр \(a\) (Crowder et al. 1994) і перехунку \(\lambda_a\) за нових параметрів:
\[\frac{\partial \ln(\lambda)}{\partial \ln(a_{i,j})} \approx \frac{\lambda_{(a + 0.01a)} - \lambda_{(a - 0.01a)}}{0.02 \cdot \lambda_a}\]
Звісно, наведений вище приклад із морською черепахою є надуманим і спрощеним. Насправді, в її популяції можна виділити наступні вікові групи: яйця, нещодавно вилуплений молодняк, дрібні молоді особини, великі молоді особини, субдорослі, та дорослі особини (Crowder et al. 1994). Спостереження за дикими популяціями показує, що стадія яєць/молодняка триває один рік і має річне виживання \(s_1 = 0.68\), потім молодняк, що вижив, переходить на стадію дрібних молодих особин, що триває із сім років і має виживання \(s_2 = 0.75\) на рік; великі молоді особини проводять на цій стадії, в середньому, ще вісім років із річним виживанням \(s_3 = 0.68\), і тоді переходять на стадію субдорослих особин, в якій проводять, приблизно, ще шість років із річним виживанням на рівні \(s_4 = 0.74\); врешті, всі особини, що дожили до цього моменту, переходять в стадію дорослих із річним виживанням на рівні \(s_5 = 0.81\) та із репродуктивним потенціалом відкласти, в середньому, \(\hat{f} = 76.5\) яєць на рік (Crouse et al. 1987). Це все можна перерахувати в ймовірності переходів між станами: якщо прийняти \(\hat{\lambda}\) за апріорний сумарний темп росту популяції (такий, який дослідник має прикинути “на око” до початку обчислень), \(T_i\) – за тривалість життєвої стадії (тут – в роках), то ймовірність особини протягом року перейти в наступну стадію можна оцінити як
\[\gamma_i = \left( \frac{s_i}{\hat{\lambda}} \right)^{T_I} - \frac{(s_i/ \bar{\lambda})^{(T_i - 1)}}{(s_i/ \bar{\lambda})^{T_i}} - 1\]
Тоді параметри матриці Леслі можна визначити як
\[ \begin{cases} p_i = s_i \times (1 - \gamma_i) \\ g_i = s_i \times \gamma_i \\ f_i = (\hat{f}_i \times p_i) + (\hat{f}_{i+1} \times g_i) \end{cases} \]
Робота Кроуз та співавторів (1987, 1994) із параметризації матриці Леслі для популяції великоголової морської черепахи виявилась доволі визначною. Вони показали, що для базової моделі власне значення становило \(\lambda \approx 0.95\) – оскільки це менше за одиницю, за вказувало на поступове вимирання популяції. Це узгоджувалось із спостереженнями за дикою популяцією, котра щороку меншає. Аналіз чутливості на цій моделі показав, що підвищення виживання гнізд та яєць черепах не надто впливало на \(\lambda\). Практично це означає, що повсюдна охорона гнізд морських черепах не є ефективною. Звісно, це не означає, що гнізда не потрібно охороняти – однак теорія вказувала на те, що якась інша життєва стадія є критичною для збереження виду. Той же аналіз чутливості/еластичності вказував, що цією стадією є дорослі особини. Отже, менеджмент охорони морських черепах, котрий фокусується винятково на охороні їх гнізд та ігнорує збереження крупніших вікових форм є беззмістовним. На основі цих робіт було розроблено регуляторні механізми, що зобов’язували рибальську індустрію до модифікації рибальських сіток – основної причини смертності молодих та дорослих черепах. Дуже скоро рибалськькі човни були оснащені спеціальними приладами, по суті, крупними решітками, котрі запобігали потраплянню великих організмів до сіток. Декілька десятиріч потому видається, що це спрацювало, й популяції морських черепах хоч і досі є під загрозою, однак, наче, стабілізувались (Jenkins 2012, Hays et al. 2025).
Чи можна в моделі Леслі ввести стохастичні елементи? Якщо коротко, то так, параметри матриці Леслі можна замінити випадковими змінними (Cáceres & Cáceres-Saez 2011). Стохастичні параметри – по суті, розподіли змінних, котрі заміняють фіксовані значення \(p_i\), \(g_i\), чи \(f_i\) – можуть мати між собою якусь кореляцію, або бути абсолютно незалежними. Математично, в таких випадках спроби аналітично отримати власні значення і власні вектори можуть виявитись великою пробоемою, але замість того моделювання може бути ітеративне. Загалом, ідея стохастичних матриць Леслі не є новою (Slade & Levenson 1982, Grant & Benton 1996), але поєднання лінійної алгебри із стохастичним моделюванням не для слабких.
Нарешті, що, якщо вам дуже хочеться використати модель Леслі, але ви не знаєте параметрів матриці? Очевидно, оцінка цих параметрів – виживання вікових груп, ймовірності їх переходів, репродуктивний потенціал – вимагає чималого об’єму даних і тривалих польових досліджень. На щастя, результати таких досліджень агрегуються в формалізовані бази даних матриць популяцій: COMADRE для тварин і COMPADRE для рослин та інших таксонів. Набори матриць Леслі із множини популяцій, що існують за різних умов середовища, можна використати в експериментах відповіді життєвих таблиць (Life Table Response Experiment, LTRE) – відносно новій родині методів статистичного умовиводу для матричних моделей, котрі дозволяють оцінити зв’язок між параметрами середовища і динамікою структурованої популяції (Hernández et al. 2023).
4.8.3 Агентні моделі
Матричні моделі є дуже зручними у використанні, адже множення матриць є елементарною операцією в більшості мов програмування. Втім, вони досі мають спільний недолік із диференційними моделями: числа є лише числами, тож ці моделі можуть згенерувати не-цілі значення (наприклад, 2.5 особини). Чи існує спосіб напряму змоделювати кожну окрему особину в популяції, із їх індивідуальними параметрами? Звісно, що існує, і цей підхід зветься агентним моделюванням (agent-based modeling, ABM, або individual-based modeling).
Напевно, перед поясненням сучасних агентних моделей варто згадати клітинні автомати (cellular automata) – математичні моделі, що складаються з дискретних клітинок в (зазвичай, двовимірному) просторі, де кожна клітинка може перебувати в одному із декількох станів, й існують визначені критерії переходів між станами з часом. Найбільш відомим і одним із найстаріших клітинним автоматом є “гра в життя” (Game of Life), де кожна клітинка в просторі може бути або живою, або мертвою, і вся динаміка системи визначається чотирма правилами для кожної клітинки, що залежать від стану восьми сусідніх клітинок (Gardner 1970, Johnston & Greene 2022):
жива клітинка, оточена менш ніж двома живими клітинками, помирає (Рис. 4.17a);
жива клітинка, оточена двома чи трьома живими клітинками, виживає (Рис. 4.17b–c);
жива клітинка, що оточена більш ніж трьома живими клітинками, помирає (Рис. 4.17d–e);
мертва клітинка, оточена рівно трьома живими сусідами, стає живою (Рис. 4.17f).
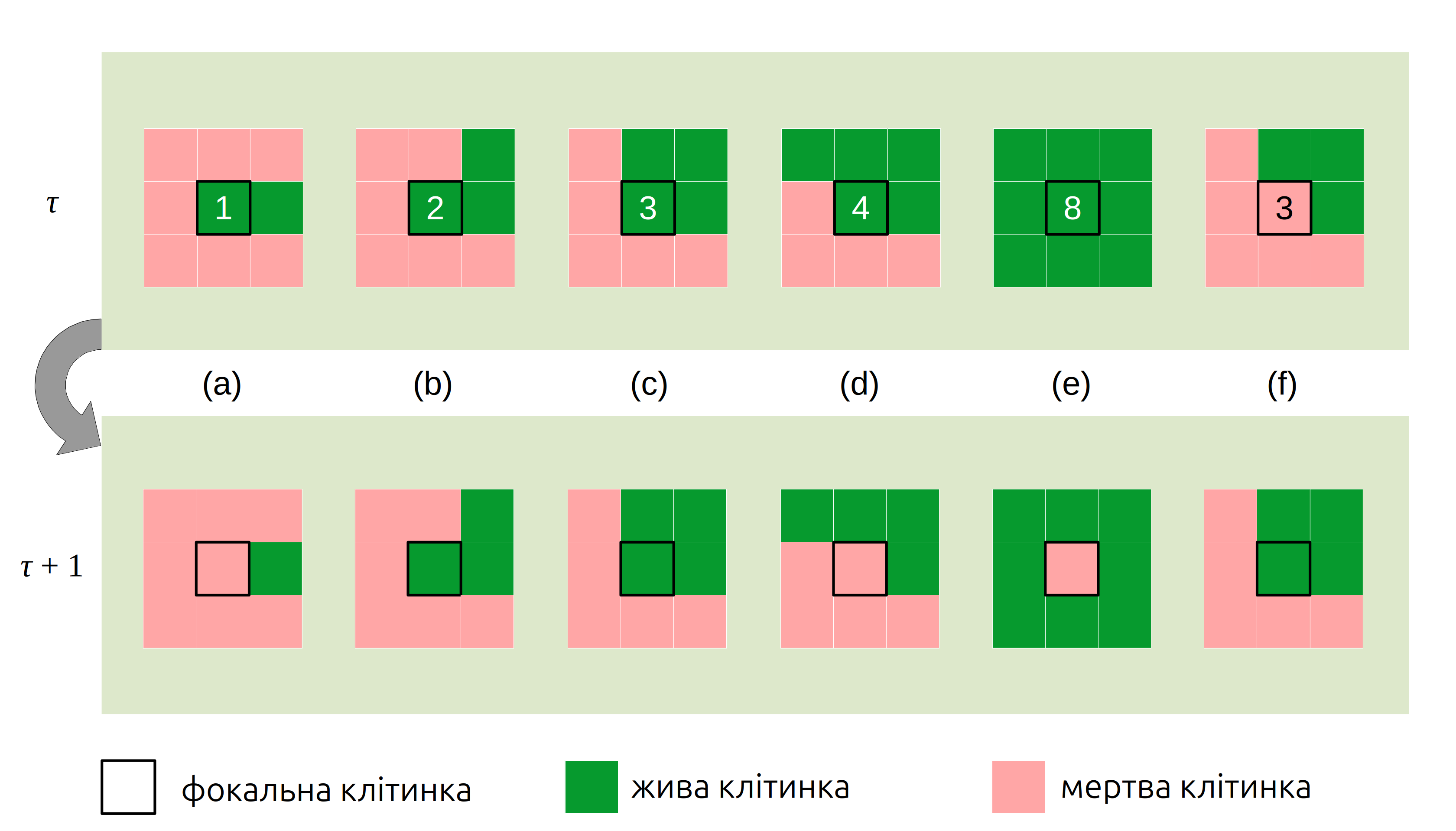
Рис. 4.17: Правила переходів між живим та мертвим станами клітинок в грі життя залежно від кількості живих сусідів в певний момент часу (позначно номером у фокальній клітинці). Ілюстрація не враховує зміни станів сусідніх клітинок.
Така модель є доволі самостійною і залежить тільки від початкових параметрів – просторової організації живих клітинок на початку симуляції. Вся подальша еволюція моделі є ізольованою від спостерігача і визначається тільки правилами переходу між станами клітинок.
Зауважте наскільки гра в життя подібна до класичної теорії метапопуляції: можна уявити, що живі клітинки відповідають локаціям, на яких присутня локальна популяція, а мертві – вакантним локаціям, на яких популяція локально вимерла. Знову ж, зверніть увагу на різницю в підходах між диференційними рівняннями і агентними моделями: класична теорія метапопуляції лише обчислювала зміну частки зайнятих локацій в часі (\(dp/d\tau\)), в той час як гра в життя моделює кожну окрему клітинку і зміну її статусу в часі. Якщо порахувати кількість живих клітинок в системі в кожен момент часу, то вийде щось на кшталт параметру в центрі уваги диференційних моделей, але в агентних моделях такий параметр є, радше, похідним результатом (тобто якщо його не обчислювати, то модель все одно працюватиме).
Очевидно, що навіть таку посту модель буде складно імплементувати “на папері”: необхідно для кожної клітинки порахувати кількість живих сусідів, прийняти рішення щодо виживання фокальної клітинки, і так повторити для кожного кроку часу. Не дивно, що розвиток подібних моделей був обмеженим розвитком комп’ютерних технологій.
В контексті агентних моделей, в грі життя ми б назвали кожну окрему клітинку агентом. Динаміка цілої моделі визначається поведінкою агентів. В агентному моделюванні нас часто цікавлять емерджентні властивості (emergence) – такі властивості моделі, які походять від поведінки агентів, але не могли б бути пояснені як сума властивостей агентів.
Одна із найперших суто агентних моделей в науковому дослідженні описувала соціальну сегрегацію (Schelling 1971). В ній агенти репрезентували, скажімо, родини, що заселяють будинки (клітинки простору). Кожен агент належить до однієї з двох можливих соціальних груп, і кожна родина намагається заселити будинок, в якому сусіди належать до тієї ж соціальної групи. На кожному кроці часу, кожна родина перевіряє частку сусідів, що належать до тієї ж групи, і якщо ця частка менша ніж певна бажана частка (наприклад, “ми не хочемо жити в будинку, якщо більш ніж половина сусідів належать до не моєї соціальної групи”), то агенти рухаються в сусідню вакантну клітинку. Симуляція триває допоки кожен агент не опиняється в такому оточенні, котре його задовільняє (тобто частка сусідів з тієї ж соціальної групи більша чи дорівнює заданій бажаній частці). Ця модель показала, що навіть низькі значення нетолерантності призводять до вираженої сегрегації, що притаманна для суспільства зі значними розбіжностями в соціо-економічному становищі: до прикладу, різні райони (neighborhoods) в містах Сполучених Штатів.
Застосування агентних моделей в екології обмежене, хіба що, фантазією. Будь-яку систему можливо змоделювати з базовими знаннями в програмуванні. Типова агентна модель складається зі (1) світу, котрий описує обмежене середовище (зазвичай, дискретний двовимірний простір із певними характеристиками кожного тайлу (tile)—чи клітинки—середовища), (2) агентів, кожен із яких має набір параметрів що або є індивідуальними і зберігаються протягом життя агента, або є змінними стану (state variable) що змінюються протягом симуляції, та (3) набору правил, що визначають взаємодію агентів зі світом, агентів між собою, рух агентів тощо. Такі правила можуть бути дуже складними і можуть включати, наприклад, елементи навчання, коли дії агентів залежать від їх попереднього досвіду, чи передбаченнями щодо сприйнятої вигоди від певних дій.
На практиці, ніщо не заважає написати агентну модель в R – зрештою, агенти і їх середовище є лише наборами даних. Втім, для візуального уявлення про агентну модель в реальному часі хорошим інструментом може видатись мова NetLogo. Великою її перевагою є існування величезної бібліотеки моделей, тож користувач навіть не потрібен мати навички програмування: просто завантажте програму і почніть бавитись із моделями із бібліотеки. Такі моделі можуть дуже навіть стати в нагоді у викладанні різних концепцій в екології, теорії еволюції, клітинної біології, біохімії, моделюванні епідемічних процесів тощо (Рис. 4.18).
.](images/netlogo.png)
Рис. 4.18: Приклад агентної симуляції популяції кроликів в NetLogo. Агенти (кролики) здійснюють випадковий рух світом, в якому випадково росте зелена травичка чи фіолетовий бур’ян. Коли кролик потрапляє на клітинку із травичкою чи бур’яном, він їх їсть і від того отримує енергію (кількість енергії від травички чи бур’янів може бути різною, в цій симуляції – 5 одиниць від травички і 0 від бур’яну). Якщо кролик отримує достатньо енергії (15 одиниць), то він/вона розмножується. Якщо кролик нічого не їсть, то настає смерть. Травичка випадково регенерується із частотою 15 нових клітинок на крок часу, бур’яни – 5. Модель кроликів-травички-бур’янів за Wilensky 2001.
Найбільша критика NetLogo полягає в тому, наскільки мультяшно це все виглядає, однак не дозволяйте цьому факту ввести вас в оману: агентні моделі є цілком валідним інструментом. Подібно до матричних моделей, агентні моделі дозволяють проводити аналіз чутливості. Єдиними застереженнями тут є те, що (1) симуляція агентної моделі сама по собі займає комп’ютерний час, адже пряме моделювання кожного окремого агенту вимагає набагато більше обчислень, аніж диференційні рівняння чи множення матриць, і (2) симуляції агентних моделей за своєю природою є стохастичними, тому кожна окрема симуляція (run) буде відрізнятись своїм результатом від інших – тому необхідно проводити повторні симуляції для кожної комбінації параметрів, що вимагає ще на порядок більше комп’ютерного часу74. Аналіз чутливості для агентних моделей може стати в нагоді для оцінки стійкості та опору системи75. Існують наступні методи оцінки чутливості агентних моделей (ten Broeke et al. 2016):
однофакторний аналіз (one-factor-at-time, OFAT) – оцінка часткових похідних результату симуляції за змін одного параметру, коли інші параметри залишаються незмінними;
глобальний аналіз чутливості (global sensitivity) – аналіз результатів багатьох симуляцій за рандомних комбінацій параметрів задля пошуку частки варіації результатів, що можна пояснити варіацією певного параметру. Для цього можна використати множинну лінійну регресію і подивитись на \(R^2\), однак точнішим методом є варіаційний аналіз чутливості (variance-based sensitivity analysis, Sobol’ method). Цей метод розглядає агентну модель як “чорну скриньку”76, якусь функцію від \(i = 1, 2, \cdots, d\) параметрів \(X_i\), що видає результат \(Y = f(X)\):
\[Y = f_0 + \sum \limits_{i=1}^d f_i(X_i) + \sum \limits_{i: i<j}^d \left[ f_{i,j} (X_i, X_j) + \cdots + f_{1, 2, \cdots, d} (X_1, X_2, \cdots, X_d) \right]\]
В такій системі, варіацію результату моделі можна розкласти як
\[\text{Var}[Y] = \sum_{i=1}^d V_i + \sum_{i:i<j}^d \left[ V_{i,j} + \cdots + V_{1, 2, \cdots, d} \right]\]
де \(V_i = \text{Var}[\mathbb{E}[Y | X_i]]\) та \(V_{i,j} = \text{Var}[\mathbb{E}[Y | (X_i, X_j)]] - V_i - V_j\) є умовними варіціями (conditional variance), і \(\text{Var}[\mathbb{E}[Y | X]]\) позначає варіацію умовного середнього (\(\mathbb{E}[Y|X]\) позначає середнє/очікування значення \(Y\) за певного значення \(X\)). На практиці, цю варіацію можна оцінити якщо розділити змінну параметру \(X_i\) на дискретні групи в порядку зростання значення (наприклад, для змінної між \(0\) і \(1\) – одна група \(0 < X_i \leq 0.1\), інша \(0.1 < X_i \leq 0.2\), і так далі) і оцінити середнє значення \(Y\) для кожної групи; варіація цих середніх буде вашим шуканим77 \(\mathbb{E}[Y|X]\). Тоді чутливість (першого) моделі до параметру можна оцінити як
\[S_i = \frac{V_i}{\text{Var}[Y]}\]
Процедура варіаційного аналізу чутливості на практиці передбачає генерування матриці випадкових значень \(\mathbf{Q}\) розміром \([N \times 2d]\), де \(d\) – кількість параметрів моделі, і \(N\) – кількість повторів симуляції (чим більше параметрів, тим більше повторів варто провести). Значення колонок, що відповідають випадковим значенням параметрів, повинні бути в діапазоні й одиницях цих параметрів (тобто, якщо в прикладі із Рис. 4.18 одним із таких параметрів є енергетична цінність трави, то випадково згенеровані значення мають бути в діапазоні від нуля до, скажімо, двадцяти). Розділимо матрицю \(\mathbf{Q}\) навпіл: позначимо \(\mathbf{A}\) як перші \(d\) колонок в \(\mathbf{Q}\), і \(\mathbf{B}\) – як колонки \((d+1, \cdots, 2d)\). Із цих двох матриць, побудуємо множину \(d\) матриць \(\mathbf{A}_\mathbf{B}^{(i)}\) де кожна \(i\)та колонка взята із матриці \(\mathbf{B}\), а всі інші колонки – з \(\mathbf{A}\). Тепер проженіть симуляцію для таких комбінацій параметрів, що відповідають рядкам в матрицях \(\mathbf{A}\), \(\mathbf{B}\), і всіх \(\mathbf{A}_\mathbf{B}^{(i)}\), і з кожної симуляції отримайте результат \(f(X)\). Тоді чутливість можна оцінити, якщо прийняти
\[\hat{V_i} \approx \frac{1}{N} \sum _{\nu = 1}^N \left[ f(\mathbf{B})_{\nu} \times (f(\mathbf{A}_\mathbf{B}^{(i)})_{\nu} - f(\mathbf{A})_{\nu}) \right]\]
де \(f(\mathbf{X})_{\nu}\) позначає результат симуляції, проведеної для такої комбінації параметрів, що описується рядком \(\nu\) в матриці \(\mathbf{X}\) (де замість \(\mathbf{X}\) може бути \(\mathbf{A}\), \(\mathbf{B}\), чи \(\mathbf{A}_\mathbf{B}^{(i)}\)).
Якщо ви до цього моменту ще не зовсім втратили розуміння що тут відбувається, ви могли трохи заплутатись, що є результатом симуляції. В агентних моделях це вирішуєте ви! Наприклад, в моделі із Рис. 4.18 результатом може бути середній розмір популяції кроликів, сумарна кількість спожитої енергії протягом популяції тощо. Фокальну метрику результату моделі варто обирати так, щоб вона якимось чином відображала екологічну сутність процесу, який ви моделюєте, але вибір такої метрики завжди залишається за дослідником. Тільки варто бути обережними із будь-якими усередненями результатів протягом тривалості симуляції, адже агентна модель займає деякий час, аби стабілізуватись (як-то на Рис. 4.18 популяція кроликів досягає біль-менш стабільної фази після приблизно сотні кроків часу, тому якщо дослідник бажає оцінити середній розмір популяції протягом симуляції, то першу сотню значень варто викинути із обчислень).
… котрі так притаманні типовим українським підручникам з екології й визначним рамкових концепціям (“ні про що”) на котрих ті базуються – на кшталт робіт Сукачова, Голубця, Раменського, Беклемишева тощо.↩︎
Важко, але не є неможливим. Наприклад, ви цілком можете використати багаторічні часові серії чисельності популяції для параметризації рівняння щільність-залежного логістичного росту, оцінити, наприклад, \(r\) та \(K\) – однак треба розуміти навіщо це робити і що це дасть. Як на мене, у більшості випадків, нічого корисного.↩︎
Тобто рівняння є різницевим (difference equation) якщо ми уявляємо час як дискретну змінну (наприклад, чисельність популяції в певний рік, де рік є дискретним кроком часу) або диференційним (differential equation) якщо час є континуальним.↩︎
Наприклад, для десятка локацій, \(p\) може приймати значення \(\{\frac{0}{10}, \frac{1}{10}, \frac{2}{10}, \cdots, \frac{9}{10}, \frac{10}{10}\}\), і тому значення на кшталт \(p = 0.23\) не може існувати.↩︎
Пригадайте, що лінійну регресію можна використати для опису нелінійних зв’язків. Наприклад, якщо вас цікавить зв’язок між змінною \(x\) та \(y\) і ви бачите, що вони пов’язані нелійнійно, а, радше, як \(y = x^2\), то вам нічого не заважає визначити нову змінну \(z = x^2\) і побудувати лінійну регресію вигляду \(y = \beta_0 + \beta_1 z\). Формула лінійна, але зв’язок – нелінійний.↩︎
Авторегресія (autoregression, AR) є доволі поширеним поняттям в часових серіях, яке визначає залежність кроку в часі від попередніх кроків із певною затримкою (lag). Ми визначаємо авторегресійний процес порядку \(p\), \(\text{AR}(p)\), як такий, в якому значення \(\tau\)-того кроку є функцією попередніх \((\tau - 1, \cdots, \tau - p)\) кроків плюс рандомна похибка.↩︎
Не-Марківський процес (non-Markovian) є таким динамічним процесом, що не виявляє властивості Маркова (Markov property) – коли майбутній розвиток процесу не залежить від історії попередніх кроків. Пригадайте, що в ланцюгах Маркова перехід в наступний стан залежить тільки від попереднього стану. У випадку не-Марківського процесу, більш ніж один передній крок впливає на наступні кроки.↩︎
В абревіації ARMA ми вже знайомі із AR – авторегресійним процесом. MA ж відповідає рухомому середньому (moving average). \(\text{MA}(q)\) – це такий процес порядку \(q\), де кожне \(i\)те значення є функцією попередніх \((i-1, \cdots, i-p)\) похибок. Моделі ARMA комбінують властивості авторегресійних процесів та процесів із рухомим середнім.↩︎
Підхід REML (restricted maximum likelihood) застосовують для оцінки нюансних параметрів (nuissance parameters) – таких параметрів, які не є в центрі уваги оцінки в статистичному тесті, наприклад, варіації. Наприклад, пригадайте, що спроба розрахунку оцінщика варіації для нормального розподілу через максимізацію функції правдоподібності призводить до упередженості оцінщика, адже він залежить від розміру вибірки. Натомість, метод обмеженої максимальної правдоподібності втрачає один ступінь вільності для кожного параметру, котрий треба оцінити (наприклад, \(\hat{\mu}\)).↩︎
Коли обчислення вимагають тривалого часу, проводити їх на персональному комп’ютері стає непрактично. Натомість, в нагоді можуть стати хмарні обчислення (cloud computing) та кластери високопродуктивних комп’ютерів (high-performance computing, HPC), до яких користувач має доступ через Інтернет. Хмарні обчислення дозволяють використовувати кластери із десятками ядер процесорів (ваш персональний комп’ютер має десь від 2 до 8 ядер), сотнями гігабайтів оперативної пам’яті, та терабайтами пам’яті. На практиці, це дозволяє користувачу запустити довготривалий процес зі свого комп’ютера і забути про нього поки він не завершиться десь на сервері. Доступність багатьох ядер вимагає, втім, паралелізації процесів (parallel computing) – за замовчунням, скрипт, скажімо, на R, виконується лінійно і використовує одне ядро процесора незалежно від того, скільки ядер доступно. Паралелізація на R вимагає використання специфічного синтаксису і окремих бібліотек, зокрема,
doParallelіforeach.↩︎Ми визначаємо стійкість (resilience) як здатність системи до відновлення після пертурбації, і опір (resistance) як здатність системи залишатись незмінною під тиском.↩︎
Чорна скринька (black box) – це погляд на модель, що ігнорує її механізми. Ми ввели вхідні параметри, модель виплюнула результат, а як – нас це не цікавить. Що під капотом моделі? Хтозна.↩︎
Варто зазначити, що існує альтернативний метод оцінки \(V_i\), де варіація умовного очікування результату оцінюється за всіх параметрів крім \(i\)того.↩︎