4.7 Метапопуляція

В попередніх розділах ми визначили поняття популяцію як групу особин, що ізольовані від інших груп. Весь попередній розділ стосується динаміки чисельності популяції, і з точки зору описаних моделей, зміна чисельності стосується цілої популяції; іншими словами, чисельність популяції є одним параметром однієї популяції. Таке уявлення передбачає, що якщо чисельність популяції змінюється, то ці зміни стосуються всіх особин одночасно і в однаковій мірі. Відтак, чисельність популяції є прикладом жартівливої “середньої температури по лікарні”⁵⁹.

Природні системи, зазвичай, гетерогенні, і усереднення параметрів завжди призводить до втрати інформації. Системи популяційного рівня не є виключенням. Можна уявити, що динаміка чисельності популяції в будь-який момент часу не є однорідною: природні популяції складаються із менших локальних популяцій, і якщо в певних локаціях популяція перебуває на стадії зростання, то інші локації в той же час можуть виражати зменшення чисельності чи навіть локальне вимирання (Andrewartha & Birch 1954). Оскільки ми вже позначили термін популяції як такий, на рівні яких відбуваються демографічні процеси, набір популяцій можна позначити терміном метапопуляція (metapopulation). На відміну від класичної моделі популяції, поняття метапопуляції передбачає, що кожна популяція в складі метапопуляції є відкритою: існує притік іммігрантів та відтік емігрантів в/із кожної популяції.

4.7.1 Загальна модель метапопуляції

Перше формальне визначення метапопуляції надав Річард Левінс як “популяція популяцій, котрі вимирають і заново колонізують середовище” (Levins 1969). Модель Левінса уявляє значний простір середовища, що утворене окремими локаціями, або клаптиками (habitat patch). Кожна локація може або не може підтримувати життєздатну популяцію виду. Не всі локації, котрі мають прийнятні умови, є заселеними: на будь-якій придатній заселеній локації популяція може вимерти, і, подібно, якщо локація є придатною але не є заселеною, то вид може колонізувати цю локацію. Отже, якщо ми подивимось на одну конкретну локацію протягом тривалого часу, то побачимо, що вид її то колонізує, то на ній локально вимирає, то знову реколонізує (Рис. 4.7).

$Динаміка заселення популяцією окремої локації є прикладом [ланцюга Маркова](\#paradigms). Дискретний шматок придатного середовища може перебувати в одному в двох станів: або заселення популяцією виду (ліворуч), або ні (праворуч); між цими двома станами існують визначені ймовірності переходів, що відповідають темпам реколонізації ($mN$) та темпам вимирання ($e$). Темпи реколонізації та вимирання позначені згідно із оригінальною моделлю Левінса.$

Рис. 4.7: Динаміка заселення популяцією окремої локації є прикладом ланцюга Маркова. Дискретний шматок придатного середовища може перебувати в одному в двох станів: або заселення популяцією виду (ліворуч), або ні (праворуч); між цими двома станами існують визначені ймовірності переходів, що відповідають темпам реколонізації ($mN$) та темпам вимирання ($e$). Темпи реколонізації та вимирання позначені згідно із оригінальною моделлю Левінса.

Метапопуляція чимось нагадує епідеміологічні процеси (Hanski 1998): в динаміці інфекційних захворювань ми маємо господарів інфекції, які можуть бути здоровими або інфікованими, а в метапопуляції такими господарями є локації, котрі можуть бути зайняті популяцією або вакантні. Формально, модель Левінса має наступний вигляд: якщо $N$ – це кількість локальних популяцій в момент часу, що утворюють метапопуляцію, $T$ – сумарна кількість локацій, котрі мають придатні для виду умови, $m$ – темп реколонізації (recolonization, яка ймовірність того, що порожня придатна локація буде заселена?), $e$ – темп вимирання (extinction, яка ймовірність того, що вид зникне із придатної локації?); тоді нові популяції заселяють порожні придатні локації із темпом $mN(1-\frac{N}{T})$ і вимирають із темпом $eN$, і отже сумарна динаміка метапопуляції виглядатиме як

\[\frac{dN}{d\tau} = mN(1-\frac{N}{T}) - eN\]

Метапопуляція такого вигляду зможе досягнути стану рівноваги тільки якщо темпи заселення дорівнюють темпам вимирання, тобто вираз вище тотожний нулю. Тоді нескладно⁶⁰ обчислити рівноважний розмір метапопуляції як $N^* = T(1 - \frac{e}{m})$. Варто зазначити, що параметр $N$ тут відповідає кількості локальних популяцій в метапопуляції, або, рівнозначно, кількості придатних локацій, що заселені видом. І локальні популяції, і локації в цій моделі є дискретними і рівнозначними: гарним прикладом може бути дошка для шашок, на якій кожна клітинка може містити одну шашку (локація є заселеною локальною популяцією) або бути порожньою (незаселеною) (Рис. 4.8). Відтак, модель метапопуляції Левінса не дає уявлення про чисельність метапопуляції в особинах⁶¹, а лише про поширення метапопуляції в середовищі.

Code

e <- 0.1
m <- 0.1

simlength = 500

mp <- vector(mode = "list", length = simlength)
mp[[1]] <- sample(x = c(0, 1), size = 100, replace = T)

for (i in 2:simlength){
  M <- m*mean(mp[[i-1]])*(1 - mean(mp[[i-1]]))
  E <- e*mean(mp[[i-1]])
  mp[[i]] <- sapply(mp[[i-1]],  function(x) {
    ifelse(
      x == 0, 
      sample(x = c(1, 0), size = 100, replace = T, prob = c(M, 1-M)), 
      sample(x = c(1, 0), size = 100, replace = T, prob = c(1-E, E))
    )
  }
  )
}

mp <- lapply(1:simlength, function(t) tibble(loc = 1:100, status = mp[[t]], time = t)) %>% bind_rows()

mp %>%
  mutate(status = as.factor(status)) %>%
  ggplot(aes(x = time, y = loc, fill = status)) +
  geom_tile() +
  scale_fill_manual(values = c("1" = "black", "0" = "white")) +
  theme_minimal() +
  theme(legend.position = "none") +
  xlab("Час, τ") + ylab("Локація")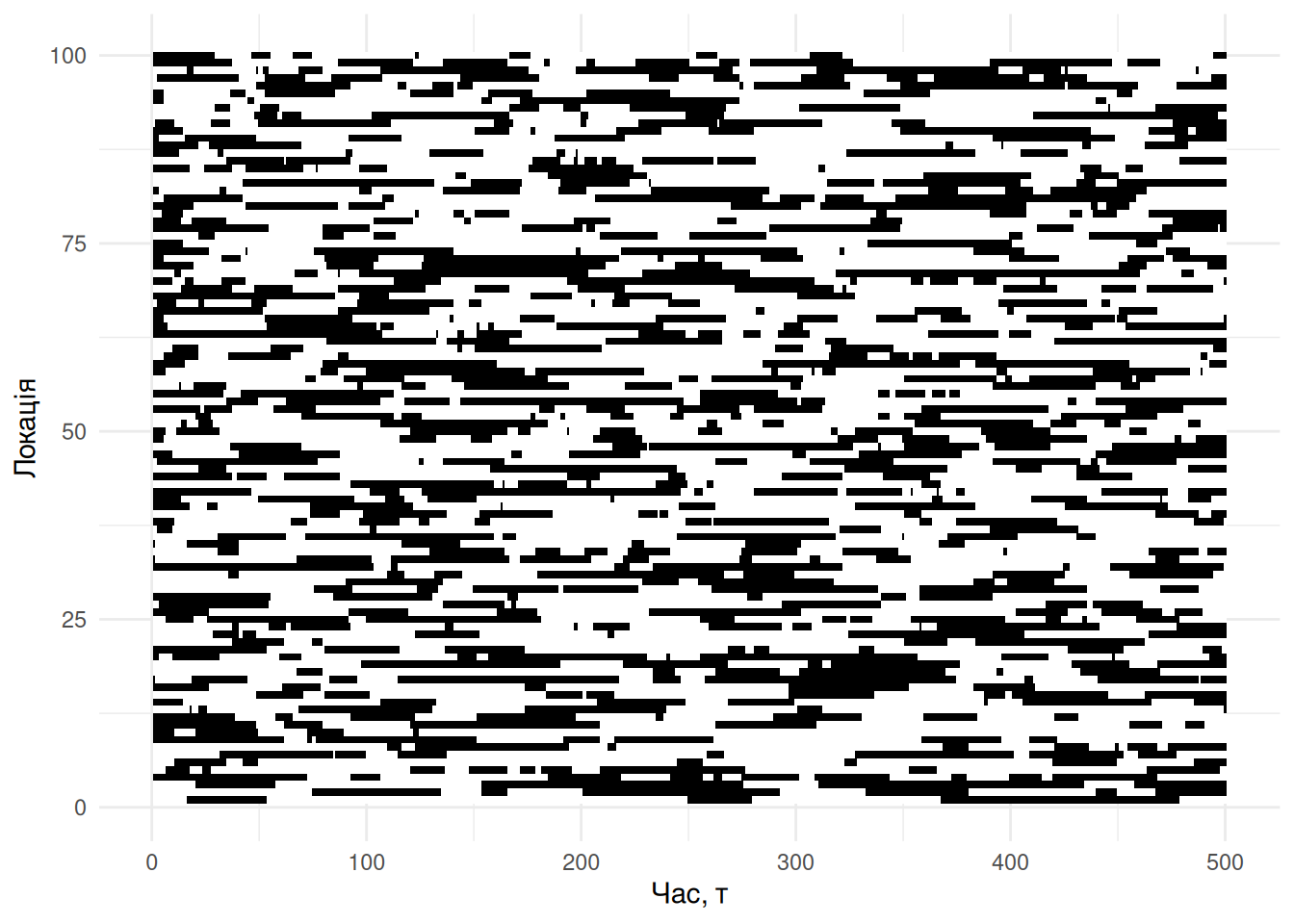

Симуляція динаміки метапопуляції в часі. Кожна із сотні локацій може бути заселена (чорний колір) чи ні. Кожен рядок візуалізує історію заселеності локації протягом часу симуляції. Параметри цієї симуляції $m = e = 0.1$.

Рис. 4.8: Симуляція динаміки метапопуляції в часі. Кожна із сотні локацій може бути заселена (чорний колір) чи ні. Кожен рядок візуалізує історію заселеності локації протягом часу симуляції. Параметри цієї симуляції $m = e = 0.1$.

Яка б ця модель не була спрощена, погляд на її параметри може дати певне уявлення про екологічні процеси. Наприклад, темп вимирання $e$, скоріш за все, залежить від умов середовища. Якщо середовище непридатне для виду, можна передбачити, що темпи вимирання будуть вищими порівняно із більш придатними середовищами. Якщо ж придатність середовища змінюється в часі, то це вноситиме варіацію до рівноважного стану метапопуляції, і $N^*$ набуватиме форму не фіксованого значення, а змінної із якимось розподілом ймовірності.

Водночас, інший параметр метапопуляції – темп міграції $m$ – навряд чи є фіксованим незалежно від дистанції між локаціями. Навпаки, можна уявити, що темп міграції між сусідніми локаціями буде набагато вищим порівняно із ізольованими локаціями. Левінс визначив цю залежність як $m = m_0 \exp[-aD]$ де $m_0$ – темп міграції за нульової дистанції (тобто між сусідніми локаціями), $D$ – дистанція між локаціями, та $a$ – фіксований параметр.

Для кращого розуміння того, що собою представляє $N$ в цій моделі, подальший розвиток концепції метапопуляції часто використовує термін $p = N/T$ – поширеність (occupancy), або частка локацій, котрі зайняті популяціями виду. Тоді модель Левінса набуває вигляду

\[\frac{dp}{d\tau} = \color{darkgreen}{mp}(1 - p) - \color{darkred}{e}p\]

із рівноважним станом $p^* = 1 - \frac{e}{m}$. Метапопуляція виживає тільки якщо $m > e$.

Модель метапопуляції Левінса має наступні наслідки (Nee & May 1992):

В стані рівноваги завжди існують незаселені придатні локації: якщо $p^* = 1 - \frac{e}{m}$ відповідає частці заселених локацій, то очевидно що $(1 - p^*) = \frac{e}{m}$ дозволяє оцінити очікування частки незаселених локацій.
Елімінація придатних локацій із середовища (наприклад, через зміну землекористування) зменшує темп росту метапопуляції. Наприклад, якщо із всіх доступних локацій вилучити частку $d$, то модель динаміки метапопуляції набуває вигляду

\[\frac{dp}{d\tau} = mp(1 - d-p) - ep\]

Існує таке значення $d$, за якого рівноважне $p$ дорівнює нулю; іншими словами, якщо вилучити забагато придатних локацій із системи, метапопуляція колапсує. Таке граничне значення $d$ називають порогом вимирання (extinction threshold).

Пізніше, модель Левінса була розвинута до врахування міжвидових зв’язків (Hanski 1983), однак, ці моделі вимагають розуміння міжвидових взаємодій і виходять за межі теми популяції одного виду, тож у цьому розділі ми їх проігноруємо. Натомість, можна вивести більш загальне формулювання моделі метапопуляції (Gotelli & Kelley 1993).

В оригінальній моделі Левінса, ефективно, є дві частини: колонізація ($\color{darkgreen}{mp}$), що є метапопуляційним процесом (адже зважується на розмір метапопуляції $p$), та вимирання ($\color{darkred}{e}$), котре є незалежним від метапопуляції. Однак, якщо:

існує “ефект рятівника” (rescue effect), коли значний розмір метапопуляції зменшує ймовірність вимирання (Hanski 1982) і потік іммігрантів скасовує локальне вимирання, модель може набути форми

\[\frac{dp}{d\tau} = \color{darkgreen}{mp}(1 - p) - \color{darkred}{e(1-p)}p\]

існує притік іммігрантів ззовні системи, наприклад, якби фокальна метапопуляція існувала на системі островів і отримувала міграційний потік із континенту (Gotelli 1991) – так званий “дощ живців” (propagule rain⁶²), коли локальні популяції отримують значний потік нових особин (спор, насіння, вегетативні живці, личинки, молоді особини тощо); тоді розмір метапопуляції не має ефекту на динаміку і модель набуває вигляду

\[\frac{dp}{d\tau} = \color{darkgreen}{m}(1 - p) - \color{darkred}{e}p\]

обидва ефекти мають місце одночасно:

\[\frac{dp}{d\tau} = \color{darkgreen}{m}(1 - p) - \color{darkred}{e(1-p)}p\]

В загальній моделі метапопуляції (Gotelli & Kelley 1993), визначмо функцію $\color{darkgreen}{\mu(p)}$, котра визначає ймовірність локальної колонізації за певного розміру метапопуляції $p$. Аналогічно, визначмо іншу функцію, $\color{darkred}{\epsilon(p)}$, котра визначає ймовірність локального вимирання. Тоді загальна модель метапопуляції набуває вигляду

\[\frac{dp}{d\tau} = \color{darkgreen}{\mu(p)} \cdot (1-p) - \color{darkred}{\epsilon(p)} \cdot p\]

У найпростішому випадку, ці дві функції (колонізації та вимирання) можна описати лінійними рівняннями:

$\color{darkgreen}{\mu(p)} = \beta_{\mu, 0} + \beta_{\mu, 1} \cdot p$ (позитивний лінійний зв’язок із $p$),
$\color{darkred}{\epsilon(p)} = \beta_{\epsilon, 0} - \beta_{\epsilon, 1} \cdot p$ (негативний лінійний зв’язок із $p$).

Ціла модель тоді набуває погрозливого вигляду

\[\frac{dp}{d\tau} = \color{darkgreen}{[\beta_{\mu, 0} + \beta_{\mu, 1} \cdot p]} \cdot (1-p) - \color{darkred}{[\beta_{\epsilon, 0} - \beta_{\epsilon, 1} \cdot p]} \cdot p\]

Задля біологічного реалізму, коефіцієнти в цій моделі повинні мати певні обмеження: $\beta_{\mu, 0}, \beta_{\mu, 1}, \beta_{\epsilon, 0}, \beta_{\epsilon, 1} > 0$ та $\beta_{\epsilon, 0} > \beta_{\epsilon, 1}$. В цій системі може існувати чотири стани рівноваги:

$p^* = \frac{\beta_{\mu, 0}}{\beta_{\mu, 0} + \beta_{\epsilon, 0}}$,
$p^* = \frac{\beta_{\mu, 0}}{\beta_{\epsilon, 0} - \beta_{\mu, 1}}$,
$p^* = \frac{\beta_{\mu, 1} - \beta_{\epsilon, 0}}{\beta_{\mu, 1} - \beta_{\epsilon, 1}}$, та
$p^* = 0$ (тотальне вимирання цілої метапопуляції).

4.7.2 Стохастичність і детермінізм в метапопуляціях

Оригінальна модель Левінса (1970) передбачала можливість стохастичної динаміки: параметр вимирання $e$ можна уявити як випадкову змінну із середнім $\bar{e}$ та варіацією $\sigma_e^2$: $e \sim \mathcal{N}(\bar{e}, \sigma_e^2)$. В такому випадку, розмір метапопуляції буде не фіксованим значенням $p$, а змінною із розподілом $\Phi(p)$. На практиці, $\Phi(p)$ можна оцінити як поширеність виду серед локацій в часі (який відсоток локацій заселено видом? порахуйте це багато разів протягом тривалого часу, і отримаєте розподіл) або як поширеність декількох екологічно подібних видів в один момент часу. Ханскі (1982) розвинув цю ідею ще далі, і математично показав, що якщо колонізація $m$ незалежна від розміру метапопуляції $p$, то модель метапопуляції зводиться до логістичного росту, в якому рівновага існує тільки коли $p^* = 0$ (тотальне вимирання) або $p^* = 1$ (тотальне домінування). Однак, якщо ввести випадкову змінну $s = m - e$, $s \sim \mathcal{N}( \bar{s}, \sigma_s^2)$, то $\Phi(p)$ матиме або рівноважний бімодальний розподіл за $\sigma_s^2 > \bar{s}$ або конвергує до $p^*=1$ за $\sigma_s^2 < \bar{s}$.

Математичний апарат стохастичної моделі метапопуляції (Hanski 1982) надав теоретичне підґрунтя до гіпотези ядра-супутників (core-satellite hypothesis). Ця гіпотеза постулює, що локальна заселеність видів пов’язана із регіональною чисельністю на рівні метапопуляції: іншими словами, регіонально рідкісні види заселяють менше локацій порівняно із регіонально багаточисельними видами. Стохастична модель Ханскі передбачає, що стохастична варіація параметрів регіональної динаміки метапопуляцій (тобто $m$ та $e$) може бути пов’язана із стохастичністю як демографічною, так і самого середовища. Згідно із цією моделлю, ми очікуємо побачити бімодальний розподіл поширеності видів поміж локацій ($\Phi(p)$): види є або дуже поширеними і мають високу регіональну чисельність (види-ядра), або поширені на небагатьох локаціях і мають низьку регіональну чисельність (види-супутники). Оскільки види-супутники виживають як невеличкі групи маленьких популяцій, їх існування значною мірою залежить від площі наявного середовища, і отже частка видів-супутників має зменшуватись в межах малих регіонів.

На цьому моменті читачу повинно бути зрозуміло, що динаміка метапопуляцій регулюється двома параметрами: темпами реколонізації та темпами вимирання. Що ж може визначати ці параметри? В загальній моделі метапопуляції обидва параметри заміщені функціями розміру метапопуляції, тобто динаміка метапопуляції залежить від самої популяції. Однак, в цю систему можна додати залежність від факторів середовища (Holt & Keitt 2000). Розгляньмо розширення оригінальної моделі Левінса Ні-Мея (Nee & May 1992):

\[\frac{dp}{d\tau} = mp(k - p) - ep\]

де $k$ – частка локацій в системі, яка придатна для фокального організму, і рівновага досягається за $p^* = k - e/m$. Оригінальна модель Левінса передбачає, що всі локації однаково доступні до реколонізації видом (Hanski 1997). До розширення Ні-Мея можна додати певний просторовий градієнт і координати локації $x$ в просторі цього градієнту. Тоді локальна динаміка популяції в точці $x$ описується як функція параметрів $m,e,k$ в цій точці:

\[\frac{dp(x)}{d\tau} = p(x) \cdot [k(x) - p(x)] \cdot m(x) - e(x) \cdot p(x)\]

Рівновага досягається якщо $p^*(x) = k(x) - \frac{e(x)}{m(x)}$.

Цікавим наслідком такого підходу є те, що динаміка метапопуляції пояснює існування меж в ареалах видів. Класично, моделювання ареалу поширення видів передбачає моделювання екологічних ніш шляхом пошуку таких локацій, на яких комбінація факторів середовища подібна до тих локацій, на яких вид задокументований. Насправді, цей підхід не стільки дозволяє моделювати поширення видів, скільки поширення придатних середовищ для цього виду. Придатність середовища сама по собі ще не означає, що вид у ньому буде траплятись, адже вид повинен до цього середовища якимось чином потрапити. Географічні бар’єри чи ізоляція таких локацій можуть стати на перешкоді: якщо “острів” придатного середовища оточений непридатним середовищем, то особини виду можуть ніколи не дістатися до такого острова. Власне, врахування демографічних процесів і динаміки колонізації й притаманні теорії метапопуляції.

Межа поширення виду повинна розділяти такі популяції, в яких рівноважний стан популяції колапсує до $p^*(x) = 0$ із локальним вимиранням (що станеться коли $k(x) < \frac{e(x)}{m(x)}$), і популяції із ненульовим рівноважним станом. Модель із просторовим градієнтом дозволяє три сценарії, за яких лінійний градієнт може призвести до існування відносно чітких меж в просторовому поширенні метапопуляції (Holt & Keitt 2000):

в градієнті доступності середовища ($k(x)$) за фіксованих $m$ та $e$, де межа ареалу відповідатиме нестачі придатного середовища, котре б дозволяло реколонізації скасувати ефект локального вимирання;
в градієнті локального темпу вимирання ($e(x)$) за фіксованих $m$ та $k$, де темпи вимирання на межі ареалу є вищими за темпи реколонізації через, скажімо, незадовільні умови середовища, часті збурення середовища, тиск хижаків чи конкурентів, чи просто низьку чисельність популяції і низький темп росту популяції;
в градієнті локального темпу реколонізації ($m(x)$) за фіксованих $e$ та $k$, де, наприклад, жорсткі умови середовища на периферії ареалу елімінують більшість особин, що намагаються поширитись, чи завдяки фізичним бар’єрам що унеможливлюють поширення виду.

Варто зауважити, що хоча й ці три процеси можуть генерувати відносно чіткі межі поширення видів, ці межі є доволі ефемерними в часі – як і, в принципі, будь-яка локальна популяція в межах метапопуляції. В будь-який момент часу будь-яка локація може бути заселена чи ні, і частка часу, коли локація заселена, й відповідає параметру $p$. Якщо в центрі ареалу можна очікувати $p \rightarrow 1$, то за межами ареалу $p \rightarrow 0$ (Рис. 4.9). Раз в іноді локації на межі ареалу все одно можуть бути заселені, хоча й це триватиме недовго – допоки локальне вимирання не візьме своє.

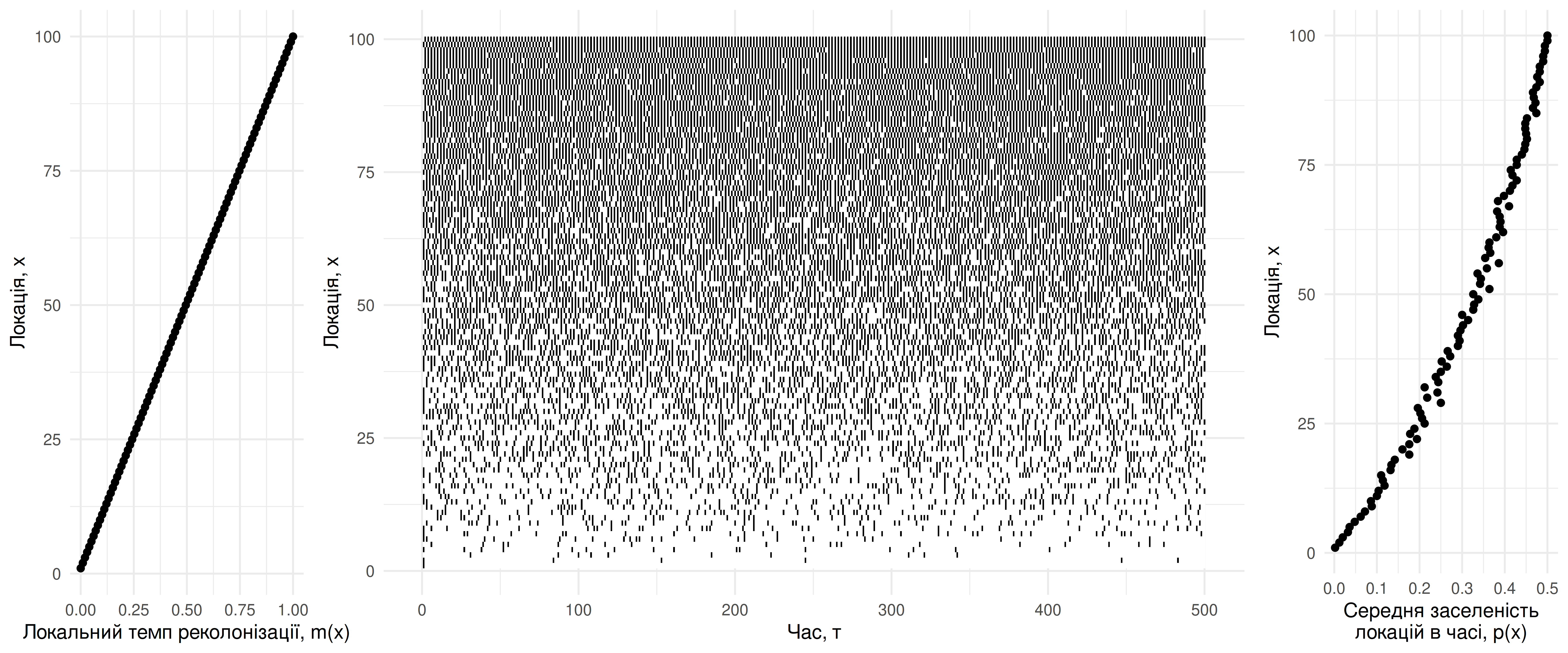
Симуляція динаміки метапопуляції в часі на просторовій межі метапопуляції. Темп реколонізації не є фіксованим, а, натомість, модельований як функція просторових координат локації, $m(x)$: градієнт змодельовано від $m(x=1) = 0$ до $m(x=100) = 1$ знизу доверху. Заселеність локації $p(x)$ можна оцінити як частку часу симуляції, протягом якого локація була заселена.

Рис. 4.9: Симуляція динаміки метапопуляції в часі на просторовій межі метапопуляції. Темп реколонізації не є фіксованим, а, натомість, модельований як функція просторових координат локації, $m(x)$: градієнт змодельовано від $m(x=1) = 0$ до $m(x=100) = 1$ знизу доверху. Заселеність локації $p(x)$ можна оцінити як частку часу симуляції, протягом якого локація була заселена.

4.7.3 Динаміка джерела–дірки та ходячі мерці

Одним із найважливіших уроків теорії метапопуляцій для охорони природи є ідея того, що в функціональній метапопуляції завжди існуватимуть порожні локації із придатним середовищем. Якщо менеджер-природоохоронець бачить середовище, над яким так довго працювали аби привабити якийсь рідкісний вид, але цього виду там так і не спостерігали – це нормально. Потрібно лише мати терпіння, цей вид там рано чи пізно з’явиться. І теорія метапопуляцій нам каже, що цей вид звідти неминуче зникне так само як і з’явився. Погляньте на секцію праворуч на Рис. 4.9 – навіть за найкращих умов ($m(x) = 1$) заселеність локацій $p(x) \approx 0.5$ – тобто в половині спостережень найпривабливіші локації порожні! Найгірше, що може вирішити менеджер, це “ну якщо цей вид не використовує цю локацію, то можна її забудувати; цей вид і так тут не трапляється, отже, втрата цього середовища ніяк на нього не вплине…” Вплине, і вплине негативно, адже втрата придатного середовища зменшить значення параметру $k$ в цій метапопуляції (у формулюванні Холта-Кейтта), і, відтак, рівноважний розмір метапопуляції зменшиться (Рис. 4.10). Втім, варто зауважити, що точна реакція метапопуляції на зникнення придатного середовища залежатиме на особливості такого зникнення (наприклад, чи зникають випадкові локації, чи вони зникають масивними кластерами?) (Hanski 1998).

Code

e <- 0.1
m <- 0.15

t <- 1:300
mp <- numeric(0)
mp[1] <- 0.01

for (time in t[-1]){
  mp[time] <- mp[time-1] + m*(mp[time-1])*(1 - mp[time-1]) - e*mp[time-1]
}

mp1 <- numeric(0)
mp1[1] <- mp[1]

for (time in t[-1]){
  mp1[time] <- mp1[time-1] + m*(mp1[time-1])*(1 - 0.1 - mp1[time-1]) - e*mp1[time-1]
}

mp2 <- numeric(0)
mp2[1] <- mp[1]

for (time in t[-1]){
  mp2[time] <- mp2[time-1] + m*(mp2[time-1])*(1 - 0.3 - mp2[time-1]) - e*mp2[time-1]
}

plot(t, mp, type = "l", xlab = "Час, τ", ylab = "Заселеність, p")
lines(t, mp1, lty = "dashed")
lines(t, mp2, lty = "dotted")
text(x = 275, y = 0.31, labels = "d = 0")
text(x = 275, y = 0.21, labels = "d = 0.1")
text(x = 275, y = 0.05, labels = "d = 0.3")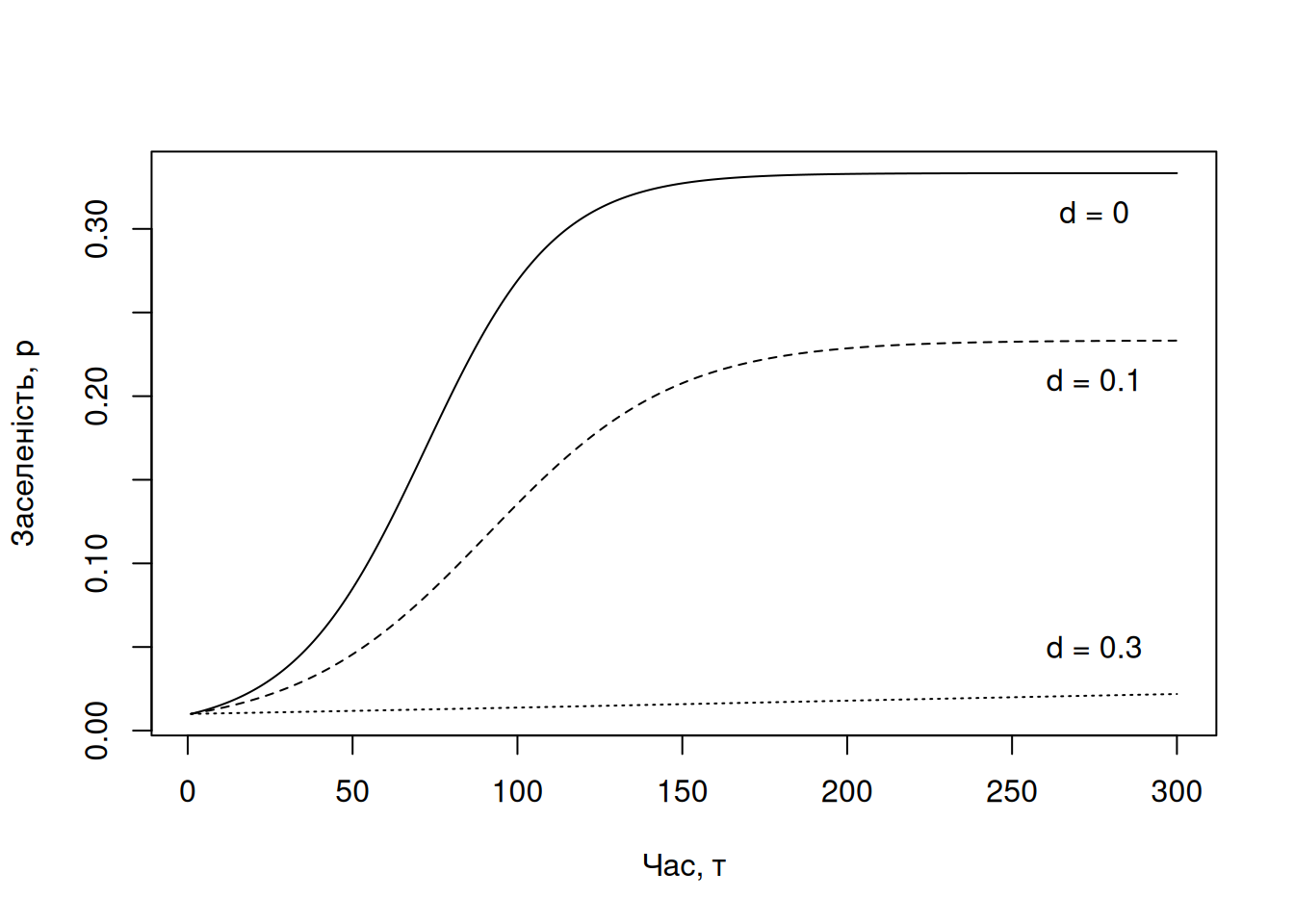

$Симуляція динаміки метапопуляції в часі за різних рівнів вилучення придатного середовища. В цій моделі вигляду $\frac{dp}{d\tau} = mp(1-d-p) - ep$ параметр $d$ відповідає частці придатних локацій, що вилучаються із середовища (наприклад, через забудову чи іншу зміну землекористування). Інші параметри моделі сталі: темп реколонізації $m = 0.15$, темп вимирання $m = 0.1$.$

Рис. 4.10: Симуляція динаміки метапопуляції в часі за різних рівнів вилучення придатного середовища. В цій моделі вигляду $\frac{dp}{d\tau} = mp(1-d-p) - ep$ параметр $d$ відповідає частці придатних локацій, що вилучаються із середовища (наприклад, через забудову чи іншу зміну землекористування). Інші параметри моделі сталі: темп реколонізації $m = 0.15$, темп вимирання $m = 0.1$.

Подібно до того, як відсутність виду на локації не означає, що вид почувається погано, із оберненою ситуацією потрібно бути обережним. Присутність виду на локації ще не означає, що цей вид перебуває в стабільній рівновазі і його чисельність не зменшується. Навпаки, навіть коли глобально метапопуляція вимирає, час від часу нові локації все одно будуть реколонізовуватись видом (хоча і з темпом меншим, аніж вони вимирають на заселених локаціях). Метапопуляційні процеси розтягнуті в часі, і реколонізація/вимирання в масштабах метапопуляції відбувається набагато повільніше, аніж локальні популяційні процеси (Hanski 1983). Метапопуляції дуже довго добираються до стану рівноваги, або й взагалі не добираються у флуктуючих умовах середовища. Та навіть якщо умови середовища залишаються стабільними, існуватимуть локальні популяції, які заселяють придатні локації коли ціла метапопуляція прямує до колапсу – ефект, що охрестили боргом вимирання (extinction debt; Tilman et al. 1994). Коли система набуває борг вимирання, локальні активні популяції являють собою “ходячі мерці” (living dead), адже їх локальне вимирання без подальшої реколонізації є лише питанням часу (Hanski 1997).

Можливо, не все так погано як воно звучить. Той факт, що динаміка метапопуляцій – тривалий процес, може стати в нагоді для ефективної охорони природи. Якщо рівноважний стан метапопуляції змістився в напрямку вимирання, у менеджерів є трошки часу, аби щось із цим зробити. Наприклад, темпи реколонізації можна підвищити, якщо якимось чином вдасться налагодити зв’язок між популяціями для обміну “живців” (propagules – не обов’язково частини рослин, що вегетативно розмножуються, а будь-яка комбінація особин, котрі можуть дати початок новій популяції) шляхом підвищення з’єднаності середовища (connectivity). Так звані екодуки, або переходи через шляхопроводи для диких тварин, є чудовим практичним методом підвищення з’єднаності між популяціями, і, відтак, допомагають підвищити рівноважну чисельність метапопуляції й запобігти її колапсу (Van Der Windt & Swart 2008, Aiello et al. 2023)⁶³.

Скільки часу є у менеджерів, аби встигнути врятувати метапопуляцію до її колапсу? По-перше, треба встановити цільовий розмір метапопуляції, за якого метапопуляція може повернутись до ненульової рівноваги. Стохастичне моделювання тут може встати у нагоді, аби обчислити, наприклад, мінімальний розмір метапопуляції, за якого вона має 95% шанс вижити протягом тривалого часу (наприклад, століття); мінімальна кількість придатного середовища може також стати цікавою змінною. По-друге, теорія метапопуляцій дозволяє оцінити очікуваний час до колапсу метапопуляції (Hanski 1997) як

\[T_M = T_L \exp[\frac{Hp^2}{2(1-p)}]\]

де $T_L$ – очікуваний час до локального вимирання популяцій (наприклад, середня тривалість часу між локальною реколонізацією і подальшим вимиранням), $H$ – кількість доступних придатних локацій, $p$ - частка заселених локацій.

Ідея популяцій-ходячих мерців може наштовхнути на думку: а чи окремі локальні популяції взагалі можуть існувати без притоку іммігрантів із метапопуляції? У деяких випадках, справді, не зовсім. У найпростішому випадку можна уявити систему із двох популяцій: обидві популяції успішно заселяють свої локації ($N = 2, p=1$) і ми припустимо що жодна із них не досягає локального вимирання. Популяції на цих локаціях пов’язані через дисперсію особин, а, отже, існує потік іммігрантів та емігрантів між цими популяціями (оскільки у нас тільки дві популяції, ми припустимо що всі емігранти із популяції 1 стають успішними іммігрантами в популяції 2). Локації, втім, відрізняються своєю придатністю (suitability): локація 1 має дуже плодорідні умови для фокального виду, але локація 2 представлена не дуже придатним середовищем. Придатність середовища відображається у внутрішніх темпах росту популяції: в першій популяції народжуваність перевищує смертність ($r_1 > 0$), однак друга популяція не настільки щаслива ($r_2 < 0$). Якби ці популяції були ізольованими, з часом друга популяція би локально вимерла. Але цього не відбувається завдяки еміграцію в неї: надлишкова смертність компенсується притоком іммігрантів. Відтак, перша популяція є джерелом мігрантів (source), а друга – діркою для них (sink), і систему цих популяції можна описати як динаміку типу джерела-дірки (source-sink dynamics). З точки зору спостережника, динаміка джерела-дірки є небезпечною для хибного висновку щодо динаміки локальних популяцій: спостережник на локації 2 побачить популяцію із більш-менш стабільною динамікою і зробить висновок, що середовище на цій локації є цілком придатним, в той час як ця локація є насправді лише гарячою точкою вимирання особин.

Якщо взяти до уваги популяції в контексті їх зв’язку із іншими популяціями, можна виділити наступні чотири типи просторової організації метапопуляцій (Harrison 1991; Рис. 4.11):

нерівноважні популяції (non-eqilibrium populations): між реколонізацією та вимиранням немає балансу (наприклад, через надмірну ізоляцію локальних популяцій), що виводить систему з рівноваги; локальні вимирання з часом призводять до глобального колапсу;
плямисті популяції (patchy populations): особини згруповані в постійні просторові кластери (наприклад, клаптики придатного середовища), однак між ними існує з’вязок і обмін генами;
класичні метапопуляції (classic metapopulations): маргінальний випадок плямистої популяції, де популяції населяють дискретні клаптики середовища, є однорідними в розмірі, і кожен клаптик середовища змінює свій стан з колонізованого на вакантний і навпаки;
континентально-острівні популяції, або популяції за типом джерела-дірки (mainland-island, source-sink populations): існує велика материнська популяція (континент), для якої ймовірністю вимирання можна знехтувати, і система менших островів, для яких притаманна динаміка класичної метапопуляції із реколонізацією/вимиранням; популяції на островах (дірках) підтримуються потоком мігрантів з континенту (джерела).

Типи просторової організації метапопуляцій (за [Harrison 1991](htpps://doi.org/10.1111/j.1095-8312.1991.tb00552.x), [Mittelbach & McGill 2019](https://doi.org/10.1093/oso/9780198835851.003.0013)).

Рис. 4.11: Типи просторової організації метапопуляцій (за Harrison 1991, Mittelbach & McGill 2019).

4.7.4 Псевдодірки й екологічні пастки

В контексті континентально-острівної динамки, або динаміки джерела-дірки, варто згадати поняття псевдодірок (pseudosinks) та екологічних пасток (ecological traps). Пригадайте рівняння логістичного росту: приріст популяції залежить від того, наскільки близько розмір популяції $N$ наближається до ємності середовища $K$, і якщо розмір популяції завеликий ($N > K$), то приріст популяції стає від’ємним – тобто чисельність популяції зменшується. У випадку динаміки псевдодірки, локальна популяція сама по собі має позитивний темп росту ($r > 0$), однак потік іммігрантів настільки значний, що сумарна кількість локальних особин із іммігрантами перевищує ємність середовища і пригнічує темпи росту популяції (Watkinson & Sutherland 1995). Якщо дисперсію організмів обмежити, то популяція псевдодірки повернеться до нормальних рівнів ($N < K$, $r > 0$), а за повного припинення імміграції питомий розмір такої популяції залишатиметься стабільним без локального вимирання.

Екологічна пастка ж утворюється коли організми дисперсують в пошуках придатного середовища, але потрапляють в такі середовища, котрі в момент пошуку виглядають придатними, однак насправді такими не є; іншими словами, непридатне середовище видається організму більш привабливим порівняно із насправді придатним середовищем (Dwernychuk & Boag 1972). Зрештою, організми намагаються утворити популяції в непридатних середовищах, що спричиняє динаміку за типом джерела-дірки. Екологічні пастки трапляються переважно серед тварин, котрі мають достатні когнітивні здібності для оцінки придатності середовища: цей процес передбачає, що організм оцінює придатність середовища і помиляється; а ефект екологічних пасток може варіювати від 100% смертності до менш помітних процесів на кшталт пригніченого репродуктивного потенціалу (Hale & Swearer 2016). Сценарій екологічної пастки часто трапляється коли середовище різко змінюється (наприклад, зменшення кормової бази, спалах в хижацтві, гніздового паразитизму тощо), а організми не встигають адаптуватись до цих змін й використовують ті ж сигнали (cues), що використовувались до змін (Robertson & Hutto 2006). Екологічні пастки для багатьох таксонів часто пов’язані із урбанізацією середовища, адже міста пропонують привабливі ресурси (наприклад, кормові ресурси, нові субстрати для гніздування тощо), хоча їх сумарна придатність має сумнівну якість (через підвищене хижацтво, ймовірність заразитись паразитами, забруднення тощо) (Zuñiga-Palacios et al. 2021).

4.7.5 Функції трапляння

Класична теорія метапопуляції передбачає, що локації, на яких трапляються популяції, є дискретними й однорідними. За виключенням континентально-острівної моделі динаміки, це передбачає, що всі середовища мають однакову площу. Аби ввести можливість варіації площі середовища, завершити цей розділ варто поняттям функцій трапляння (incidence functions). Термін був запропонований Джаредом Даямондом для мультивидових угруповань в контексті дозволених (permissible) та заборонених (forbidden) комбінацій видів на острівних екосистемах: “види, що складають угруповання, обираються через дифузну конкуренцію та їх ніші й чисельності підлаштовуються таким чином, аби підходити одне одному й перешкоджати інвазійним видам” (Diamond 1975). Сумарно, функція трапляння описує ймовірність трапляння виду як функцію сторонніх факторів, наприклад, площі середовища чи присутність інших видів. Сама ідея дозволених/заборонених комбінацій видів швидко піддалась критиці, адже дозволені й заборонені комбінації видів можуть утворюватись випадково (Connor & Simberloff 1979), однак новіший аналіз емпіричних систем показав, що реальні комбінації видів в угрупованнях, скоріше, невипадкові (Gotelli & McCabe 2002).

Припустімо (Hanski 1992), що (1) трапляння виду на острові чи клаптику середовища є динамічним через повторні вимирання та реколонізацію із континенту; (2) єдиними процесами, що залежать від площі клаптику, є колонізація та вимирання; (3) варіація в придатності середовища незалежна від його плоші; (4) вид перебуває в стані рівноваги між колонізацією та вимиранням. Якщо позначити площу середовища як $A$, тоді ймовірність колонізації становитиме $\mu(A)$, ймовірність вимирання – $\epsilon(A)$. Функцію трапляння тоді можна визначити як

\[J(A) = \frac{\mu(A)}{\mu(A) + \epsilon(A)}\]

В цілому, ймовірність колонізації не повинна дуже залежати від площі і бути сталою ($\bar{\mu}$). Натомість, ймовірність вимирання залежить від розміру популяції, а розмір популяції – від площі середовища, тому ймовірність вимирання можна визначити як $\epsilon(A) = \frac{e}{x}$ де $\{e, x\}$ є фіксованими параметрами із яких $x$ визначає чутливість ймовірності вимирання до площі середовища. Тоді функція трапляння набуває вигляду

\[J(A) = \left[ 1 + \frac{e/\bar{\mu}}{A^x} \right]^{-1}\]

В подальшому розвитку цієї моделі, Ханскі (1994) аргументував, що ймовірність реколонізації залежить від дистанції між джерелом мігрантів (континентом) та клаптиком середовища (островом) як $\mu = q \cdot \exp[-\beta D]$, де $q$ відповідає ймовірності реколонізації за нульової дистанції, а $D$ – дистанція (відповідно, $\beta$ є лише сталим коефіцієнтом). Тоді функція трапляння визначатиметься як

\[J(A, D) = \left[ 1 + \frac{e \cdot \exp[-\beta D]^{-1}}{A^x} \right]^{-1} = \left[ 1 + \frac{e \cdot \exp[\beta D]}{A^x} \right]^{-1}\]

Із такої моделі можна вилучити припущення про існування джерела мігрантів (континенту), і звести її до простої метапопуляції. Визначмо $M_i$ як кількість іммігрантів, що прибувають до клаптика $i$. Тоді ймовірність колонізації із фіксованим параметром $y$ становить $\mu = 1 - \exp [-yM_i]$, або, якщо прийняти $M_i$ за розмір живця, $\mu = \frac{M_i^2}{M_I^2 + y^2}$. Аби прив’язати $M_i$ до розмірів і локацій існуючих популяцій (очікувано, живці із близький та великих популяцій будуть більшими, аніж з далеких і малих), визначмо $M_i = \gamma S_i$ де $\gamma$ – це фіксований параметр, а

\[S_i = \sum\limits_{j=1}^n \iota_j \exp[-\alpha d_{ij}] A_j\]

де $\iota_j$ дорівнює одиниці для зайнятого клаптика $j$ та нулю якщо він вакантний, $d_{ij}$ – дистанція між клаптиками $i$ та $j$, а $\alpha$ – це виживання живців під час їх дисперсії через дистанцію $d_{ij}$. Отже, якщо прийняти $y^* = y/\gamma$ як комбінацію двох параметрів,

\[\mu = \left[ 1+ \left( \frac{y^*}{S_i} \right)^2 \right]^{-1}\]

Врешті, функція трапляння тоді матиме наступний вигляд:

\[J_i = \left[ 1 + \left( 1+\frac{y^*}{S_i}\right)^2 \frac{e}{A_i^x}\right]^{-1}\]

Таку систему можна ітерувати як ланцюг Маркова для оцінки траєкторії зайняття придатних локацій і оцінки ймовірності вимирання із часом, особливо якщо доступність й площі придатних середовищ не є стабільними. Варіювання початкових параметрів ітерацій можуть дозволити знайти альтернативні точки рівноваги системи (Hanski 1998).

В частини пацієнтів гарячка, інша частина – мертві в морзі. Середня температура по лікарні 36.6 °C.↩︎
Приймемо що $mN(1 - \frac{N}{T}) = eN$, тоді \[m \frac{N}{N}(1 - \frac{N}{T}) = \frac{eN}{N} \Rightarrow m(1 - \frac{N}{T}) = e \Rightarrow \\ \Rightarrow 1 - \frac{N}{T} = \frac{e}{m} \Rightarrow \frac{N}{T} = 1 - \frac{e}{m} \Rightarrow N = T(1 - \frac{e}{m})\].↩︎
Зверніть увагу, втім, на подібність оригінальної моделі метапопуляції Левінса $\frac{dN}{d\tau} = mN(1-\frac{N}{T}) - eN$ до класичного логістичного росту $\frac{dN}{d\tau} = rN(1-\frac{N}{K})$.↩︎
Propagule – це черговий англомовний термін, який важко перекласти. В оригінальному значенні це дійсно позначає живець – частину пагона рослини, яку можна використати для вегетативного розмноження. В більш загальному ж сенсі цей термін позначає будь-який біологічний матеріал, який здатний виконати функцію поширення виду і утворення нової популяції. Такими структурами можуть бути спори бактерій та грибів, насіння рослин (наприклад, анемохорних, тобто що поширюються вітром), соридії лишайників, личинки безхребетних, молодняк хребетних тощо. Такі живці беруть участь у дисперсії, або поширення виду (dispersal) – ще один англомовний термін, що не хоче піддаватись перекладу. Дисперсія виду не є тим самим, що міграція, адже міграція видів є типово циклічною. Зазвичай, під дисперсією мають на увазі рух молодих особин із місця їх народження до місця розмноження (натальна дисперсія, natal dispersal).↩︎
Як не іронічно, за п’ять років життя в Сполучених Штатах я жодного разу не бачив подібну структуру на власні очі.↩︎