5.1 Трофічні ланцюги і мережі
Очевидно, популяції не існують в ізоляції. Класичні моделі росту популяції—експоненційний, логістичний ріст—є виключно феноменологічними, тобто такими, що можуть підбудуватись під спостереження реальних систем, однак не дають жодного уявлення про механізми їх функціонування.
Взяти, до прикладу, щільність-залежний ріст. Класична екологія часів Лека та Елтона78 разом зі здоровим ґлуздом кажуть, що популяції повинні мати певні механізми щільність-залежної регуляції; без них, експоненійний ріст популяції швидко спричинив би мальтузіанську катастрофу, коли популяція вичерпала б наявні ресурси і колапсувала до вимирання, або, як писав Дарвін, популяція будь-якого виду за умов експоненійного росту би швидко вкрила планету товстим шаром біомаси. Отже, щільність-залежна регуляція повинна існувати? В 1948 році Девідсон та Андерварта провели експеримент із спостереження за популяцією трипсів—комах-шкідників троянд—в контрольованих умовах, і виявили що зовнішні чинники на кшталт гетерогенності середовища й мікроклімату є набагато кращими предикторами росту популяції за власне ріст популяції (Davidson & Anderwartha 1948). Невдовзі вийшла книга із назвою “Поширення й чисельність тварин” (Anderwartha & Birch 1954), що на тривалий час стала догматичною працею в екології тварин, і містила чітку аргументацію щодо того, чому щільність-залежні механізми регуляції популяцій бракують емпіричної підтримки. Не дивно, що така позиція викликала багаторічні дебати в екології щодо того, чи популяції регулюються в щільність-залежній чи щільність-незалежній манері. Сьогодні ми вважаємо, що істина десь посередині: популяції флуктують в щільність-незалежній манері більшість часу, однак щільність-залежні механізми стають особливо важливими коли популяції наближаються до екстремальних станів (занадто високої або занадто низької чисельності). В цілому, не варто виключати можливість існування щільність-залежних механізмів.
Моделі логістичного росту і тета-логістичного росту є чудовими прикладами феноменологічних моделей. В загальному вигляді, щільність-залежний ріст можна уявити як
\[\frac{dN}{d\tau} = rN \cdot f(N, \cdots)\]
де \(f(N, \cdots)\) є якоюсь функцією чисельності популяції \(N\) і додаткових параметрів (\(\cdots\)): наприклад, у випадку логістичного росту таку функцію можна записати як \(f(N, K) = 1 - (N/K)\), а тета-логістичного росту – як \(f(N, K, \theta) = 1 - (N/K)^{\theta}\). Чи ці моделі описують щільність-залежність? Звісно, адже темп росту популяції є функцією від \(N\), тобто щільності популяції. Чи вони пояснюють механізми щільність-залежної регуляції? Абсолютно ні.
Якими можуть бути механізми регуляції популяцій? Із попереднього розділу можна витягнути декілька: стохастичність абіотичних факторів середовища, демографічна стохастичність популяції, внутрішні популяційні процеси як-то динаміка смертності чи репродуктивного успіху. Жоден із цих механізмів не є щільність-залежним у вузькому сенсі. Навіть такі ефекти як зміна міжвидових зв’язків залежно від щільності популяції чи підвищена смертність від хижаків чи паразитів за високої щільності не є настільки щільність-залежними як, радше, щільність-модульованими. Насправді, ефект щільність-залежності проявлятиметься через сторонні фактори: в найпростішому випадку, висока щільність популяції зменшуватиме доступність ресурсів, що збільшує смертність й зменшує темпи розмноження, і відтак детермінує темп росту популяції. Отже, механістичне моделювання щільність-залежної динаміки популяції неможливе без врахування міжвидових зв’язків: кормової бази з одного боку і природних ворогів – з іншого, обидва з яких також є популяціями.
Кожна окрема популяція не існує в ізоляції, а, радше, існує в контексті інших популяцій. Найпростішим поглядом на такі зв’язки є трофічний компонент – хто кого їсть. В спрощеному уявленні, трофічні зв’язки спричиняють переміщення речовини й енергії між популяціями. Очевидно, енергія повинна звідкись братися в такій системі: зазвичай, це стається завдяки енергії сонячного світла і фотосинтезу. Відтак, перший трофічний рівень складатиметься із зелених рослин, і цей рівень часто позначають як продуценти (primary producers), котрі накопичують енергію в хімічних зв’язках органічних сполук і використовують наявні в середовищі поживні речовини. Звісно, замість енергії сонця може використовуватись енергія неорганічних сполук (так званий хемосинтез), однак такі випадки є виключенням із глибоководних екосистем гідротермальних джерел. Продуценти стають їжею для організмів, котрі не здатні до фото- чи хемо-синтезу: консументів (consumers), котрі можуть бути організовані в декілька порядків від травоїдів (herbivores) до хижаків (carnivores) і аж до верхівкових хижаків (apex predators – таких хижаків, що не виступають жертвою для жодного іншого виду). Оскільки всі організми в якийсь момент помирають, і їх мертві тіла містять органічні сполуки із певною енергетичною цінністю, якісь організми еволюціонували в редуцентів (decomposers), котрі розкладають складні органічні сполуки в простіші, що можуть бути використані продуцентами в якості поживних речовин.
Із такого уявлення про трофічний ланцюг (food chain) як спрямований потік трофічної енергії крізь послідовність трофічних ланок що починається із базального виду (продуценту чи наявної в середовищі органічної речовини) і закінчується консументом вищого порядку (Martinez 1991) може виникнути цілком логічне питання: якщо в трофічний ланцюг вноситься відносно стабільний потік енергії (сонячне світло), то навіть за неефективного засвоєння енергії (а фотосинтез дійсно засвоює лише невелику частку світлової енергії) куди ця енергія дівається? Насправді, цю дилему нескладно вирішити якщо врахувати фізіологію будь-якого організму: базовий метаболізм вимагає енергії. На будь-якому трофічному рівні, більшість енергії не запасається у вигляді біомаси, а витрачається на життєздатність організмів. Отже, коли один організм-хижак із біомасою \(m_1\) їсть інший організм-жертву із біомасою \(m_0\), приріст біомаси хижака \(m_1\) становитиме лише частку від \(m_0\) – цю частку можна позначити як ефективність трансферу енергії (transfer efficiency). Для задокументованих водних екосистем, ефективність трансферу енергії складає від 2% до 24%, із середнім значенням 10.13% (Pauly & Christensen 1995).
Звідси і береться магічні 10% зі шкільних прикладів екологічних пірамід: біомаса консумента другого порядку становитиме одну десяту від біомаси другого порядку, біомаса консумента першого порядку – одну десяту від продуцента тощо. Трансфер енергії в трофічному ланцюзі можна уявити як піраміду біомаси, піраміду чисельності організмів, чи піраміду енергії (Elton 1927). Звісно, емпірична оцінка трансферу біомаси чи чисельності є набагато простішою, аніж енергії.
Трофічні ланцюги є лінійними структурами: енергія переходить від одного продуцента до одного рослинноїдного консумента, від цього консумента – до хижака, і так до верхівкового хижака. Всі види в трофічному ланцюзі є абсолютними спеціалістами. Хоч екологічні спеціалісти й існують в природі, ланцюги із виключно спеціалістів будуть нестабільними, адже збурення в популяції бодай одного трофічного рівня викличуть збурення в трансфері енергії між усіма рівнями. Натомість, природні популяції часто мають альтернативні джерела ресурсів; хижаки можуть мати більш ніж один вид жертви, в той час як види на нижчих трофічних рівнях можуть споживатися різними хижаками. Відтак, якщо угруповання визначити як комбінацію особин різних видів в межах визначеного середовища, то відповідну трофічну мережу (food web) можна визначити як комбінацію всіх трофічних зв’язків між видами в угрупованні. Варто відмітити, що поняття трофічного виду відрізняється від біологічного виду: якщо декілька біологічних видів мають ідентичних хижаків і ідентичні жертви, то їх можна об’єднати в один трофічний вид (Briand & Cohen 1984). В трофічній мережі можна визначити верхівкові хижаки (top predators, хижаки без хижаків), проміжні види (intermediate species, хижаки для одних видів і жертва для інших), та базальні види (basal species, жертва без жертви), а трофічний зв’язок (trophic link) – як зареєстроване поїдання одного виду іншим. Математично, трофічна мережа є прикладом графу із орієнтованими зв’язками.
Трофічну мережу можна описати декількома параметрами: кількістю трофічних видів, або вузлів в мережі (\(S\)), кількістю зв’язків між видами (\(L\)), зв’язаністю мережі (connectance, \(L/S^2\)) тощо. Кількість зв’язків в мережі пропорційна до кількості видів, і стабільні мережі часто характеризуються переважанням прямих зв’язків між базальним і верхівковим рівнями без залучення проміжних видів (Cohen & Briand 1984). Варто зазначити, що всеїдність може помістити види на декілька трофічних рівнів одночасно, що може внести додаткову заплутаність в трофічні мережі. В реальних мережах всеїдність не є поодинокими випадками: хоча й більше половини видів займають один трофічний рівень, на трофічних рівнях вище за продуцентів і травоїдів трофічні мережі стають заплутаними мережами всеїдних організмів (Thompson et al. 2007). Втім, навіть заплутані трофічні мережі є доволі малими і мають ступінь кластеризації близький до випадкового (Dunne et al. 2002).
5.1.1 Стабільність трофічних мереж
Дослідження трофічних мереж вимагає їх стандартизованого опису. Зображувати хто кого їсть, звісно, можна зручно за допомогою графів (види як вузли і трофічні зв’язки – як стрілочки між ними), але статистичні підходи не доросли до аналізу таких малюнків. Роберт МакАртур79 в 1955 році формалізував математичну репрезентацію трофічних мереж як систем трофічних зв’язків \(p_{i, j}\) між видами \(i\) та \(j\) як таких, що описують частку біомаси виду \(j\), котра завдячує споживанню виду \(i\) (MacArthur 1955). Наприклад, якщо хижак \(T\) споживає два види жертви, \(B_1\) і \(B_2\), із рівною ймовірністю, то можна визначити \(p_{B_1, T} = p_{B_2, T} = 1/2\): половина біомаси хижака походить від споживання одної жертви, і половина – від іншої. Отже, трофічні мережі можна зобразити із зазначенням трансферу енергії, як на Рис. 5.1.
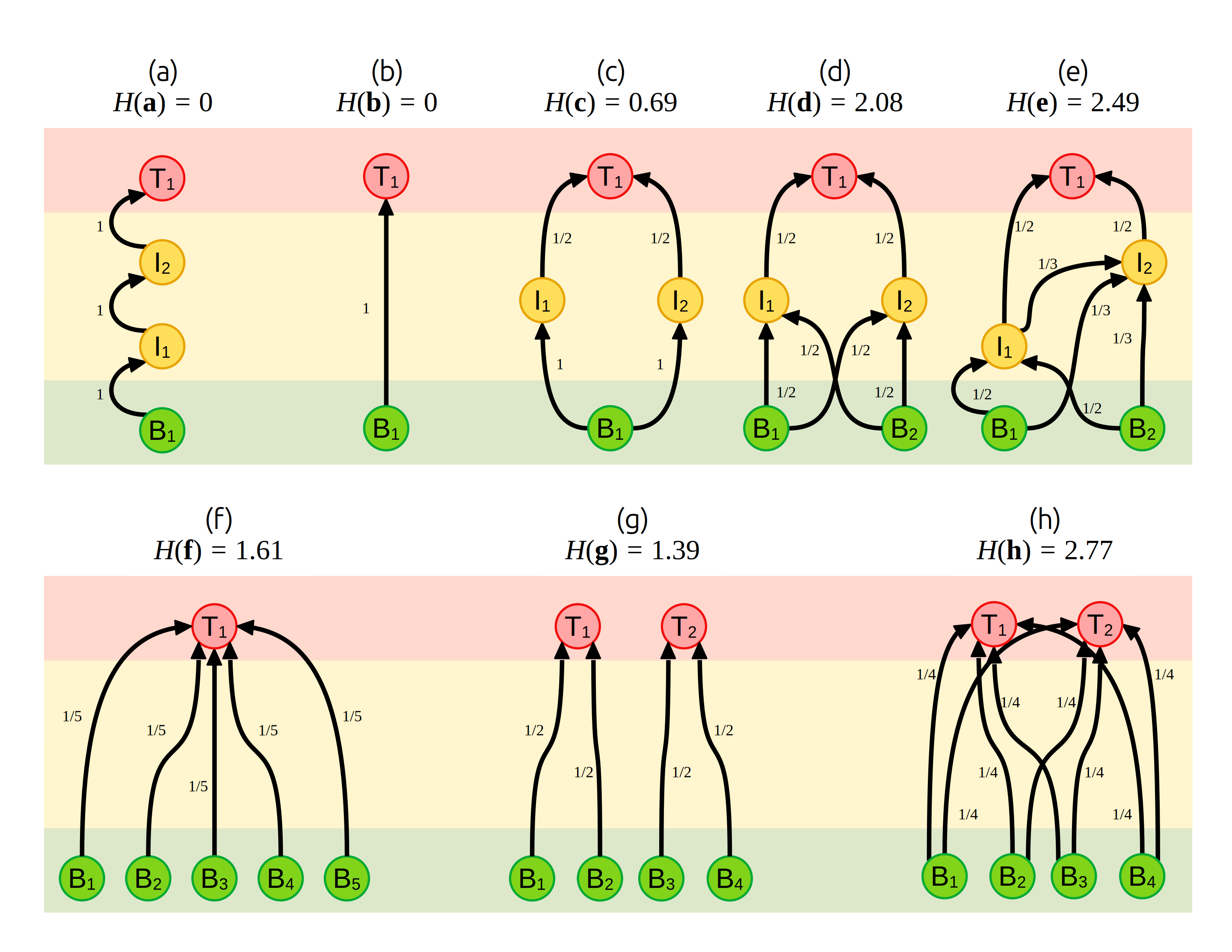
Рис. 5.1: Трофічні мережі різної складності і їх стабільність, оцінена як індекс Шенона \(H = - \sum_j p_{i, j} \log (p_{i, j})\) для трансферів енергії (\(p_{i, j}\), числа біля стрілок). Базальні види позначено як \(B\), проміжні види – як \(I\), й верхівкові хижаки – як \(T\). Нижній рядок (f–h) наводить три трофічні мережі із фіксованої кількості видів, \(S = 6\).
Трофічні мережі можна зобразити як матриці, в котрих рядки представляють види-жертви і колонки – види-хижаки. Наприклад, трофічну мережу на Рис. 5.1-c можна зобразити як матрицю вигляду
\[ \mathbf{c} = \begin{array}{cc} & \begin{array}{ccc} B_1 & I_1 & I_2 & T_1 \end{array} \\ \begin{array}{ccc} B_1 \\ I_1 \\ I_2 \\ T_1\end{array} & \left[ \begin{array}{ccc} \color{gray}{0} & 1 & 1 & \color{gray}{0} \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & 1/2 \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & 1/2 \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & \color{gray}{0}\end{array} \right]\end{array} \]
а складнішу мережу з Рис. 5.1-е як
\[ \mathbf{e} = \begin{array}{cc} & \begin{array}{ccc} B_1 & B_2 & I_1 & I_2 & T_1 \end{array} \\ \begin{array}{ccc} B_1 \\ B_2 \\ I_1 \\ I_2 \\ T_1\end{array} & \left[ \begin{array}{ccc} \color{gray}{0} & \color{gray}{0} & 1/2 & 1/3 & \color{gray}{0} \\ \color{gray}{0} & \color{gray}{0} & 1/2 & 1/3 & \color{gray}{0} \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & 1/3 & 1/2 \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & 1/2 \\ \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & \color{gray}{0} & \color{gray}{0} \end{array} \right]\end{array} \]
Зверніть увагу на те, що сума колонок завжди дорівнює одиниці. Відтак, МакАртур (1955) аргументував що трофічна мережа є прикладом ланцюга Маркова. Для повноти формалізації, необхідно ввести наступні умови до трофічної мережі: (1) кількість енергії, що вноситься в мережу, є сталою в часі: (2) тривалість часу, на котрий енергія затримується на певному виді перед трансфером на наступний трофічний рівень, є сталою в часі і між видами; (3) розмір популяції виду безпосередньо і без затримки реагує на зміни у кількості внесеної енергії; та (4) кількість енергії, що покидає трофічну мережу, дорівнює новій внесеній енергії, тобто питома зміна енергії системи дорівнює нулю. Якщо ці умови виконані, трофічна мережа досягне певного рівноважного стану незалежно від початкових параметрів на кшталт біомаси окремих видів чи кількості нової енергії. При тому, що така рівноважна система буде прикладом ланцюга Маркова, її можна вичерпно описати через рівноважні темпи трансферу енергії \(p_{i, j}\).
Стабільність трофічних мереж, на думку МакАртура, залежить від невизначеності трансферу енергії. Наприклад, у мережі на Рис. 5.1-а невизначеність переходів енергії є нульовою: у енергії немає іншого вибору, як перейти від \(B_1\) до \(I_1\), від \(I_1\) до \(I_2\), і врешті від \(I_2\) до \(T_1\). Те саме стосується простішої мережі на Рис. 5.1-b. В обох випадках, флуктуації розміру популяції на будь-якому трофічному рівні викличуть збурення на всіх інших рівнях, і тому ці системи є виключно нестабільними. Натомість, у трофічній мережі на Рис. 5.1-с існує певна невизначеність трансферу енергії: вид \(T_1\) може отримати енергію від виду \(I_1\) чи \(I_2\) із рівною ймовірністю. В такій системі, якщо, скажімо, коливання чисельності одного базального виду \(B_1\) стають критичними і цей вид вимирає, верхівковий хижак \(T_1\) може переключитись виключно на жертву \(I_2\), яка залежить від базального виду \(B_2\). Отже, навіть за вимирання одної гілки цієї мережі, інша буде існувати – тобто мережа є доволі стабільною.
Для оцінки стабільності мереж, МакАртур запозичив метод оцінки ентропії з теорії інформації. В теорії інформації, ентропія відповідає невизначеності інформації, що записана одному із \(n\) можливих станів змінної. Для однієї одиниці інформації, ентропія визначає наскільки несподіваним є її зміст. Ентропію інформації можна описати індексом Шенона, також відомим як індекс Шенона-Вінера чи індекс Шенона-Вівера (Shannon index, Shannon-Wiener index, Shannon-Weaver index), котрий часто використовують як індекс біорізноманіття:
\[H = - \sum_{i}^n \left[ p_i \cdot \log (p_i) \right]\]
Наприклад, в системі з однієї чесної монетки (тобто де \(p_{аверс} = p_{реверс} = 0.5\)), монетка є носієм інформації, і міру несподіванки в результаті підкидання можна оцінити як \(-[(0.5 \cdot \log_2(0.5)) + (0.5 \cdot \log_2(0.5))] = 1\). Якщо ж монетка нечесна, скажімо, \(p_{аверс} = 0.9 \Rightarrow p_{реверс} = 0.1\), то несподіванки стає набагато менше бо ж ми очікуватимемо аверс частіше, аніж реверс: \(-[(0.9 \cdot \log_2(0.9)) + (0.1 \cdot \log_2(0.1))] \approx 0.47\). У випадку використання двійкового логарифму \(\log_2\), одиницями ентропії є біти (bit), й індекс Шенона описує очікувану кількість бітів інформації на одиницю інформації. Втім, це не забороняє використовувати інші логарифми на кшталт десяткового чи натурального. У всякому разі, варто зазначити що індекс Шенона не має визначеної розмірності і може приймати будь-яке значення від 0 (абсолютна визначеність інформації) до \(\log(n)\).
Використання МакАртуром індексу Шенона для оцінки невизначеності переходу енергії в трофічній мережі є рідкісним прикладом адекватного використання цього індексу в екології, адже він оцінює те, для чого і був створений – ентропію системи. Стабільність трофічної мережі зростатиме зі зростанням невизначеності трансферу енергії в ній, адже це спричинятиме можливість альтернативних трофічних ланцюгів в системі за випадку флуктуацій чисельності одного виду. Чим більша стабільність трофічної мережі, тим меншими будуть наслідки втрати одного виду для цілої системи. Відтак, для трофічної мережі \(\mathbf{X}\) що складається із \(L\) трофічних зв’язків, її стабільність можна описати як
\[H(\mathbf{X}) = - \sum_{j}^L p_{i, j} \cdot \log (p_{i, j})\]
Звідси ми і можемо розрахувати значення стабільності на Рис. 5.1: наприклад, для трофічної мережі (c), \(H(\mathbf{c}) = - 2 \cdot[1 \cdot \log(1)] + 2 \cdot [0.5 \cdot \log(0.5)] \approx 0.69\). Із такого визначення стабільності можна вивести декілька передбачень щодо трофічних мереж:
стабільність збільшується з кількістю видів \(S\), адже це збільшиить кількість трофічних зв’язків в системі (\(L\));
за сталої кількості видів жертв, стабільність збільшується із кількістю хижаків (Рис. 5.1-d,e);
однакова стабільність може спостерігатись за великої кількості спеціалістів та малої кількості генералістів;
за сталої кількості видів, стабільність збільшується зі складністю трофічної мережі (Рис. 5.1-f–h).
Здавалось би, на тезі “більше видів = стабільніша екосистема” чи “складніша трофічна мережа = більша стабільність” варто було б зупинитись. Як-не-як, такий теоретичний висновок актуалізує охорону природи: збереження видів підвищить видове різноманіття, відтак, складність трофічних мереж, відтак, стабільність екосистем. Однак, не так швидко. За два десятки років після аналізу стабільності мереж МакАртура, теоретичний еколог і математик Роберт Мей80 опублікував монографію під назвою “Стабільність і складність модельованих екосистем” (May 1973), в котрій було сконструйовано модельні трофічні мережі як випадкові комбінації видів із випадковими міжвидовими зв’язками. Такі модельовані мережі за збільшення кількості видів тяжіли до стану хаотичної динаміки, в той час як простіші моделі мали вищу стабільність. Це, зрештою, не дивно, адже математичні моделі із багатьма ступенями вільності є доволі непередбачуваними, і ми можемо очікувати що складні системи будуть нестабільними.
Однак, чи можна генералізувати висновки Мея на реальні трофічні мережі? Мабуть, не дуже: на відміну від моделей Мея, реальні трофічні мережі мають невипадковий розподіл інтенсивності81 взаємодій; незначна частка пар видів мають сильні зв’язки, і трофічні мережі переважно утворені множиною слабких зв’язків між видами – хижаки зрідка виключно харчуються лише одним типом жертви (Bascompte et al. 2005). Зв’язки між видами в трофічних мережах також невипадкові, і часто утворюють модулі й підмережі. Відтак, досі є підстави вважати що складність трофічних мереж забезпечує їх стабільність.
5.1.2 Регуляція згори-донизу і знизу-догори
Отже, популяції не існують в ізоляції, а є частинами складних трофічних мереж. Усвідомлення цього факту дозволяє нам краще розуміти щільність-залежну регуляцію чисельності популяцій і робити передбачення щодо динаміки популяції.
От, наприклад, в дев’яностих роках минулого сторіччя уряд Південної Африки задався питанням: як можна збільшити вилов хеку північноафриканського (Merluccius capensis) в південно-східному Атлантичному океані? Риба ця приносить чимало прибутку, але сумарний вилов цього виду помітно спадав за останні двадцять років. Із класичної теорії динаміки популяції ми знаємо, що відновлення рибних ресурсів можна пришвидшити, якщо збільшити приріст популяції. Але що визначає приріст популяції хеків – чи їм потрібно більше макрелі та дрібних риб для корму? чи, ба, окрім рибалок хеків виловлює хтось ще? Тоді увагу уряду привернули місцеві морські котики (Arctocephalus pusillus): одна особина за день може з’їдати стільки хеків, скільки важить сам морський котик, і втрату хеків від пащі цих тварин на рік можна оцінити в 2 млн тон – стільки ж, скільки виловлюють південноафриканський рибальський флот! За такої ситуації можна інтуїтивно припустити, що штучне зменшення популяції морських котиків (наприклад, через відстріл) має вивільнити популяції хеків від надлишкового тиску хижаків, і це дозволить збільшити вилов риби вдвічі.
Втім, варто розуміти, що трофічні мережі є доволі складними і їх зміни можуть призвести до неочікуваних наслідків. Аналіз локальних трофічних мереж із океану поблизу Південної Африки показав, що елімінація морських котиків навряд чи допомогла б із відновленням популяції хеків. Хоча й між цими двома видами існує виражений трофічний зв’язок, морські котики також харчуються потенційними конкурентами та природними ворогами хеків, через що сумарний прямий та непрямий вплив морських котиків на хеків не є очевидним (Yodzis 2001).
Трофічні зв’язки всякого окремого виду в трофічній мережі із нижчими і вищими трофічними рівнями підіймають питання: з якого боку регуляція чисельності популяції є важливішою? В контексті трофічної мережі можна передбачити два можливих напрямки регуляції:
згори-донизу (top-down), коли чисельність популяції реагує на зміни в чисельності видів на вищих трофічних рівнях (наприклад, коли збільшення чисельності хижака спричиняє надмірний тиск на популяцію жертви), та
знизу-догори (bottom-up), коли чисельність фокальної популяції визначається, в першу чергу, доступними харчовими ресурсами (наприклад, коли чисельність травоїдних організмів обмежується наявними рослинними ресурсами в екосистемі).
5.1.3 Трофічні каскади
Регуляція згори-донизу і знизу-догори найбільш яскраво проявляється в трофічних каскадах – змін структури цілої трофічної мережі за зміни в одному трофічному рівні (Рис. 5.2).

Рис. 5.2: Приклади трофічних каскадів за регуляції згори-донизу і знизу-догори: зміна чисельності одного трофічного рівня (наприклад, через полювання на хижака чи надмірний врожай продуцентів) викликає зміни на всіх трофічних рівнях, а, відтак, і на цілі ландшафти.
У випадку регуляції знизу-догори, зміни в структурі трофічної мережі можна передбачити із припущення екологічних пірамід. Якщо уявити, що біомаса кожного трофічного рівня складає 10% від біомаси попереднього, то біомаси всіх трофічних рівнів можна обчислити якщо знати тільки біомасу продуцентів. Відтак, зміни чисельності продуцентів викличуть пропорційні зміни в чисельності консументів першого порядку, ті – зміни в чисельності консументів другого порядку, і так аж до верхівкових хижаків; такий ефект доміно і називають каскадом. Можна інтуїтивно очікувати, що повна елімінація найнижчого трофічного рівня викличе колапс цілої екосистеми.
Випадки регуляції згори-донизу, втім, є більш класичними в уявленні про трофічні каскади: у системі із трьох трофічних рівнів, як на Рис. 5.2, зменшення чисельності хижака викликатиме вивільнення травоїдів від тиску хижацтва. За таких умов, оскільки смертність в популяції травоїдів зменшена, їх популяція починає збільшуватись. Оскільки більша популяція травоїдів повинна чимось харчуватись, це викликає зменшення популяції продуцентів. Каскад досягає базового рівня трофічної мережі, і всі трофічні рівні піддаються ефекту зменшення чисельності одного хижака. Звісно, каскад може працювати і в інший бік: якщо чисельність хижака збільшується, то чисельність травоїдів зменшиться, що вивільнить продуцентів від надмірного випасу, і чисельність продуцентів збільшиться.
Існує безліч прикладів трофічних каскадів, однак, найбільш класичний із них: це калан морський, також відомий як морська видра (Enhydra lutris). Ці тварини їдять рибу, морських молюсків, але одна із їх улюблених страв – це морські їжаки (Рис. 5.3). Хоч морські їжаки виглядають незграбними й малорухливими, ці голкошкірі повільно і впевнено поїдають ламінарієві бурі водорості (особливо Macrocystis), які ростуть у висоту з декілька десятків метрів і утворюють густі підводні “ліси” (kelp forests), що створюють важливе середовище для морського біорізноманіття.


Рис. 5.3: Двійко каланів морських (Enhydra lutris) сплять на поверхні океану, поки їх улюблена їжа, морський їжак Strongylocentrotus purpuratus, переховується в щілинах між камінням (Природний заповідник Пойнт Лобос, Каліфорнія).
З часів колонізації Північної Америки, на каланів полювали заради їх хутра, через що вид ледь не вимер. На початку 20 сторіччя видобуток каланів заборонили, і популяції поступово повернулись до своїх нормальних рівнів. Дослідники помітили, що між присутністю каланів та чисельністю ламінарій існує певний зв’язок: виглядає, що калани контролюють популяції морських їжаків, що не дозволяє надмірного випасу бурих водоростей; водночас, за відсутності каланів екосистеми підводних лісів занепадають і виглядають як підводні пустелі вкриті морськими їжаками. Ба більше, така історія повторилася в 1990-х роках поблизу Алеутських островів на заході Аляски, навіть коли калани були присутні. Виявляється, місцеві косатки (Orcinus orca) навчились полювати на каланів, що створило трофічний каскад з чотирьох рівнів: косатки зменшили трофічний ефект каланів, що збільшило чисельність морських їжаків, що зменшило чисельність водоростей (Estes et al. 1998).
Окрім трофічних каскадів за механізмами регуляції згори-донизу чи знизу-догори, варто також виокремити субсидовані каскади (subsidy cascade): штучні субсидії (наприклад, підгодівля чи штучні гніздівлі) в популяції будь-якого трофічного рівня окрім найнижчого чи найвищого можуть викликати ефекти трофічних каскадів. Яскравим прикладом може бути свиня дика (Sus scrofa) в Малайзії: відходи від пальмових плантацій стали своєрідною субсидією для популяції свиней, це за два десятки років спричинило помітний занепад рослинності, котру свині використовують для лежанок (Luskin et al. 2017). Втім, субсидії не обов’язково мають бути штучними: наприклад, осідання поживних речовин на дні водойм чи в ґрунті може залежати від особливостей рельєфу, і варіація таких субсидій має потенціал в покращенні розуміння варіації інтенсивності зв’язків в трофічних мережах (Leroux & Loreau 2008).
5.1.4 Гіпотеза зеленого світу
Чи може теорія трофічних ланцюгів, мереж, і каскадів пояснити структуру угруповань? У 1960 році було опубліковано спільну статтю Нельсона Хейрстона, Фредеріка Сміта, та Лоуренса Слободкіна, котра намагалась дати відповідь на це запитання; ця стаття дала початок дебату щодо гіпотези, що біомаса продуцентів переважає всі інші трофічні рівні – так званої гіпотези зеленого світу (world is green hypothesis), або, за ініціалами авторів, HSS-гіпотези (Hairston et al. 1960).
HSS починається із спостереження, що темпи накопичення копалин є настільки малими порівняно із темпами фотосинтезу, що ними можна знехтувати. Відтак, майже вся енергія фотосинтезу циркулює крізь біосферу, а отже всі організми обмежені харчовими ресурсами. Навіть якщо популяція не є напряму обмежена ресурсом, то вона повинна бути обмежена трофічним рівнем на рівень нижче від ресурсу (із попереднього прикладу трофічного каскаду, якщо калан не обмежений морськими їжаками, то він має бути обмежений бурими водоростями). Водночас, продуценти навряд чи обмежені травоїдами чи нестабільністю зовнішніх умов: випадки повного, вичерпного перевипасу є дуже рідкісними, і наземні екосистеми завжди мають високу біомасу рослин. Ні, якщо продуценти не обмежені травоїдами, то вони мають бути обмежені власними ресурсами, наприклад, водою чи світлом. Якщо ми приймаємо, що популяції продуцентів стабільні, тоді й регуляція травоїдів не може бути пояснена доступністю корму – ми щойно визначили, що корм завжди доступний. Отже, популяції травоїдів регулюються наступним трофічним рівнем (хижаками, паразитами, природними ворогами). Оскільки тиск хижаків є визначним для регуляції травоїдів, тоді міжвидова конкуренція на цьому рівні має бути низькою.
Загалом, HSS спрощує трофічну мережу до всього трьох рівнів: продуцентів, травоїдів, та хижаків. В такій моделі (Mittelbach & McGill 2019),
за відсутності хижаків вищого рівня, хижаки регулюються конкуренцією за здобич (травоїдів);
популяції травоїдів пригнічені хижаками і не можуть вичерпати продуцентів;
оскільки продуценти вивільнені з-під регуляції травоїдів, їх чисельність близька до максимальної і регулюється конкуренцією.
Із HSS можна зробити два головних висновки: по-перше, якщо така модель відповідає дійсності, то продуценти мають бути наймасовішим трофічним рівнем (світ – зелений); по-друге, механізми регуляції чисельності популяції залежать від трофічного рівня. Звісно, HSS-гіпотеза викликала чималий дебат і конструктивну критику (наприклад, чому тоді рослини так багато інвестують в захист від поїдання через колючки чи хімічні репеленти?), однак ідея про стрибки механізмів регуляції між трофічними рівнями була повернена до життя через два десятки років формалізованою моделлю Оксанена та ін. (1981) (Рис. 5.4).
). Коли лінія нахилена, можна вважати що ця популяція переважно регулюється конкуренцією (знизу-догори), коли вона горизонтальна -- тиском вищого трофічного рівня (згори-донизу). (За [Mittelbach & McGill 2019](https://doi.org/10.1093/oso/9780198835851.003.0011)).](bookdown-demo_files/figure-html/fig-hss-1.png)
Рис. 5.4: Загальні висновки про рівноважні чисельності трофічних рівнів за різної складності трофічної мережі в моделі Оксанена та ін. (1981). Коли лінія нахилена, можна вважати що ця популяція переважно регулюється конкуренцією (знизу-догори), коли вона горизонтальна – тиском вищого трофічного рівня (згори-донизу). (За Mittelbach & McGill 2019).
Модель Оксанена та ін. є системою диференційних рівнянь, котрі намагаються передбачити рівноважні біомаси різних трофічних видів в градієнті потенційної первинної продуктивності (potential primary productivity) – максимального рівня біомаси, якого можуть досягнути продуценти за певних умов. У злагоді із HSS, цю величину можна виразити через, скажімо, доступність поживних речовин чи добрив, як-то нітрогену в ґрунті. В зоні 1 (Рис. 5.4), продуцент є єдиним трофічним рівнем в мережі, і його біомаса, очікувано, збільшується із доступністю лімітуючого ресурсу (чим більше добрив ми внесемо в ґрунт, тим більшої біомаси рослин можна очікувати). Втім, якщо в трофічну мережу внести травоїдів (зона 2), біомаса рослин буде ними швидко споживатись, і ця біомаса одразу потрапляє на другий трофічний рівень: відтак, хоча й травоїди напряму не вживають добрива, збільшення потенційної продуктивності збільшує біомасу травоїдів, в той час як питома біомаса рослин не змінюється. За додавання нового трофічного рівня—хижака—механізми регуляції популяцій знову перестрибують на один рівень (зона 3). Тепер травоїди регулюються хижацтвом, що дозволяє продуцентам вийти з-під контролю випасання і нарощувати біомасу за більшої доступності лімітуючого ресурсу. Подібні переключення відбуватимуться і за подальшого нарощення трофічного ланцюга (наприклад, зона 4).
Варто розуміти, що хоча й модель HSS виглядає так, ніби популяції різних трофічних рівнів перебувають під контролем або механізмів згори-донизу, або знизу-догори, ці механізми не є взаємно виключними. Наприклад, за сценарію субсидій в рівень травоїдів в умовах зони 3 на Рис. 5.4, можна було б очікувати що біомаса травоїдів збільшиться навіть коли їх чисельність регулюється тиском хижаків: насправді, механізми згори-донизу (хижаками) та знизу-догори (ресурсом) перебувають в балансі, і зміщення будь-якого із них впливатиме на трофічні рівні.
5.1.5 Не тільки трофічні мережі
Уявлення про трофічну мережу як про граф, котрий можна переписати в матрицю, і різноманітні методи опису мереж (наприклад, через коефіцієнт зв’язаності) можна не обмежувати трофічними зв’язками, а й описувати інші екологічні мережі. Найбільш популярними випадками використання мереж зв’язків є опис мутуалістичних взаємодій (наприклад, запилення комахами квіткових рослин) чи зв’язків між паразитами/паразитоїдами із їх господарями (Vilà et al. 2009, Dorado et al. 2011, Dunne et al. 2013, Albrecht et al. 2014) (Рис. 5.5).
, відтворено із дозволу авторки).](images/sophia.png)
Рис. 5.5: Приклад мутуалістичної мережі запилювання між квітковими рослинами (ліворуч) і к осами (праворуч) в Рівненському природному заповіднику (Pytel-Huta 2023, відтворено із дозволу авторки).
Дві теми в досліджені не-трофічних мереж є особливо популярними, втім, вони не є принципово відмінними від мереж трофічних. По-перше, чи видове багатство мережі впливає на її стабільність. В контексті запилювання, таке питання є доволі важливим з природоохоронної точки зору: чи можна забезпечити стабільність угруповань продуцентів за рахунок підтримки угруповань запилювачів? Дійсно, сьогодні ми спостерегаємо “кризу запилення” (pollination crisis), переважно, через історію використання агресивних інсектицидів проти шкідників сільсько-господарських культур та носіїв патогенів; зменшення чисельності та видового різноманіття запилювачів загрожує не лише природному різноманіттю квіткових рослин, але й харчовим культурам (Aizen et al. 2019, Shivanna et al. 2020). Бі більше, питання різноманіття-стабільності стосується не лише запилювачів: виглядає, що паразити так само можуть підвищувати зв’язаність трофічних мереж (Dunne et al. 2013, Laferty et al. 2006).
По-друге, цікавим питанням є що визначає вразливість мереж до інвазійних видів. Знову ж, ця тематика не є специфічною для не-трофічних мереж. Навпаки, теорія інвазій була започаткована Чарльзом Елтоном – того самого дослідника, що ввів в екологію поняття трофічної піраміди (в наступній секції ми знову згадаємо це ім’я в контексті розвитку поняття ніші). В його книзі “Екологія інвазій тваринами та рослинами” (1958), Елтон використав вже знайомий нам аргумент щодо стабільності мереж як функції їх складності: складні мережі є насичені міжвидовими взаємодіями, і відтак новому виду має бути складніше вклинитись в таку мережу (Richardson & Pyšek 2007). Коли ж інвазія успішна, в мережах рослин і запилювачів виглядає, що інвазійні рослини привертають більшу увагу запилювачів порівняно із аборигенними рослинами, однак це не впливає на зв’язаність мутуалістичних мереж (Vilà et al. 2009). Інвазійні рослини часто є генералістами в сенсі запилювачів, порівняно із більш спеціалізованими аборигенами, що дозволяє їм вклинитись в мутуалістичні мережі, і навіть якщо зв’язаність цілої мережі залишається сталою після інвазії, це не означає що структура мережі не змінюється: навпаки, інвазійні генералісти перебирають на себе зв’язки аборигенних видів, що зрештою може закінчитись їх вимиранням (Albrecht et al. 2014).
Щодо специфіки не-трофічних мереж порівняно із трофічними, варто зрозуміти маленьку відмінність і відображенні даних про них. Трофічні мережі можна уявити як квадратні матриці, у яких рядки й колонки є ідентичними і кожне значення відображає інтенсивність трофічного зв’язку. Трофічні зв’язки можуть існувати навіть між одним і тим же видом (канібалізм). Ба більше, кількість трофічних рівнів в трофічних мережах стає неінформативним параметром, адже один вид може одночасно перебувати на декількох рівнях. У випадку ж не-трофічних мереж, рівнів не існує взагалі, але під фокусом є попарні зв’язки із двох наборів видів: рослин і запилювачів, паразитів і господарів тощо. Відтак, матриці що відображають такі мережі не обов’язково мають бути квадратними, а рядки не є ідентичними до колонок (рядки можуть відповідати рослинам, колонки – запилювачам, чи навпаки).
5.1.6 Угніздованість та модулярність
“Огри мають шари. Цибуля має шари. Доганяєш? Ми багатошарові!”
— Шрек
Мережі попарних зв’язків на кшталт рослин і їх запилювачів чи паразитів та їх господарів (або будь-яких інших попарних зв’язків, скажімо, поширеності видів на островах) можна описати через їх структуру. Двома поширеними параметрами в дослідженнях таких мереж, котрі дозволяють оцінити наскільки вони випадково організовані, є їх угніздованість та модулярність (Рис. 5.6).
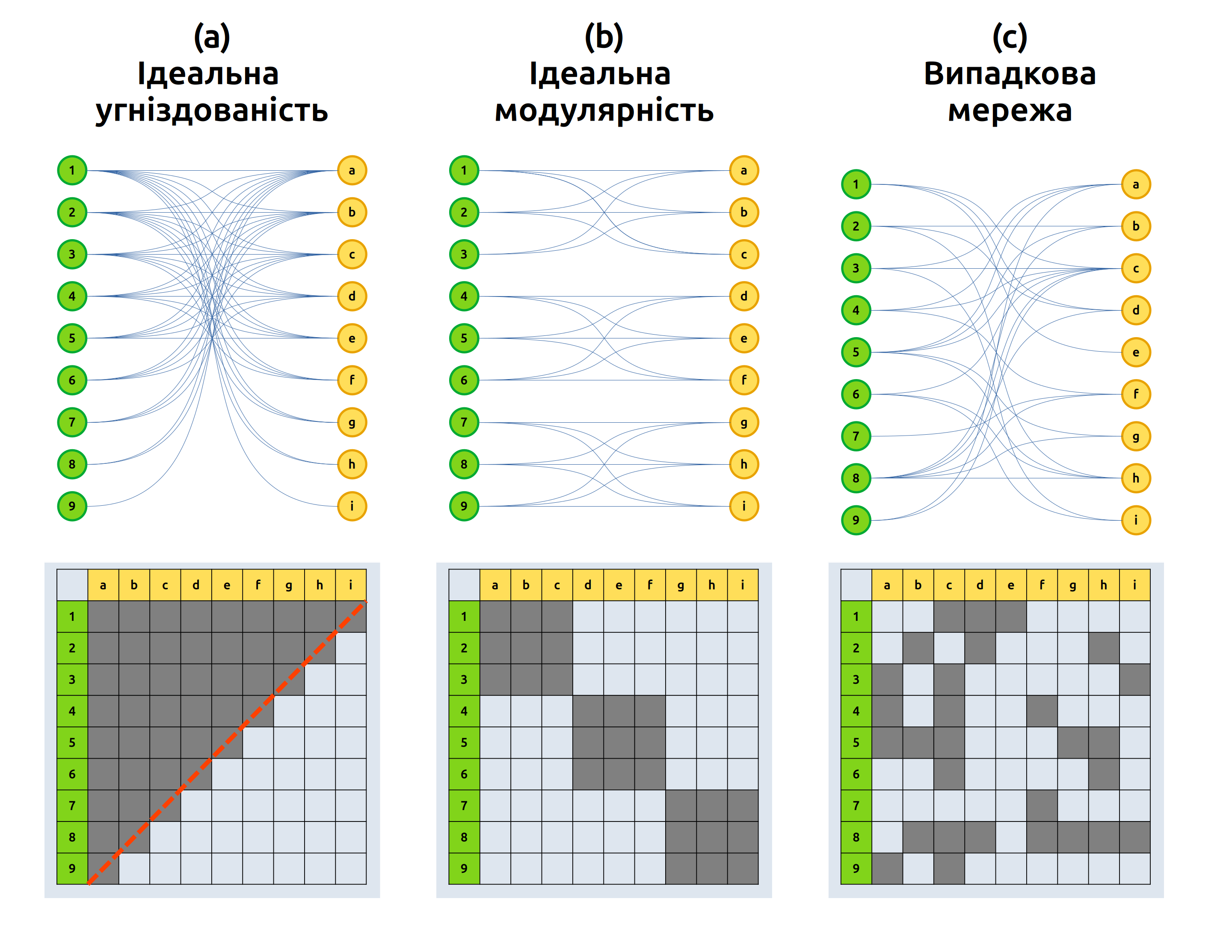
Рис. 5.6: Попарні мережі із ідеальними ступенями угніздованості та модулярності. Реальні мережі виглядатимуть не настільки добре організованими, а, скоріше, десь посередені між ідеальною угніздованістю-модулярністю та випадковими зв’язками.
Угніздованість (nestedness) описує наскільки зв’язки, утворені одним видом, є підмножиною зв’язків іншого виду. В ідеально угніздованій мережі, кожен вид взаємодіє із підмножиною більш генералістичного виду: мережа, наче цибулина, складається із менших і менших підмножин зв’язків. Аби оцінити, наскільки угніздованою є емпірична мережа, варто взяти до прикладу матрицю, що її відображає, і відсортувати її колонки за кількістю зв’язків (наприклад, щоб найбільший генераліст був в першому рядку і найбільший спеціаліст – в останньому). Тоді в матриці варто намалювати ізокліну – таку лінію, що відображала б ідеальну угніздованість (для квадратної матриці ізокліною була б діагональ цієї матриці). Тоді кількість зв’язків відсутніх ліворуч від ізокліни і кількість наявних зв’язків праворуч від неї відображатимуть, наскільки ця мережа далека від ідеальної угніздованості. Нормалізоване відхилення від ідеального випадку називають температурою \(T\), що варіює від 0 (ідеальна угніздованість) до 100 (випадкова структура) (Atmar & Patterson 1993): тоді угніздованість можна оцінити як \((100 - T)/100\). Природні мутуалістичні зв’язки між рослинами і тваринами мають доволі високу температуру, що означає що вони організовані не випадково, а в угніздованій манері (Bascompte et al. 2003).
Модулярність (modularity) представляє інший спосіб невипадкової організації мереж. В ідеально модулярній мережі можна виокремити виражені кластери зв’язків, що означатиме що види утворюють зв’язки з одним набором видів, але уникають утворення зв’язків з іншими. Оцінка модулярності мереж потребує використання доволі складних алгоритмів із пошуку кластерів, і саму модулярність можна оцінити як відношення зв’язків в межах кластерів до зв’язків між кластерами: \(\sum_{s} \frac{l_s}{L} - \left( \frac{L_s}{2L} \right)^2\) для кластерів \(s\) де \(L\) – кількість усіх зв’язків в мережі, \(l_s\) – кількість зв’язків в межах кластеру (тобто такі, що не виходять за його межі), \(L_s\) – кількість зв’язків усіх елементів кластеру (тобто включно із зв’язками, що виходять за межі кластера) (Fortunato & Barthélémy 2007). Модулярність мережі не зовсім варто вважати альтернативою угніздованості: мережа може бути одночасно угніздованою і модулярною, особливо за низької зв’язаності (Fortuna et al. 2010).
Девід Лек (David Lack) вважав, що розмір кладки яєць птахів пов’язаний із географічною широтою через тривалість світлового дня: триваліший день дозволяє отримати більше ресурсів й корму для майбутнього потомства, отже, більша кладка є оптимальною для збільшення репродуктивного успіху (Lack 1947). Ця школа думки дала початок зв’язку між теорією історії життя й еволюційною біологією та природнім добором, і цей зв’язок вимагає постулювання щільність-залежної регуляції популяцій (Ricklefs 2000). Чарльз Елтон (Charles S. Elton) вважав, що популяції тварин існують в такому собі “балансі природи”, що проявляється в циклічних флуктуаціях розміру популяції навколо якогось рівноважного рівня, що передбачає щільність-залежну регуляцію (Elton 1924).↩︎
Це далеко не остання згадка про Роберта МакАртура (Robert H. MacArthur), одного із найбільш впливових екологів-теоретиків угруповань 20-го сторіччя. За своє відносно коротке життя цей учень Гатчінсона та Лека мав значущий внесок в теорію острівної біогеографії, теорію ніш, моделювання розподілу чисельності видів, теорію співіснування, моделювання взаємодій хижак-жертва, теорію оптимального харчування тощо.↩︎
Той самий Роберт Мей (Robert May), що вивів теорію хаоса із дискретної моделі росту популяції.↩︎
Як оцінити інтенсивність трофічних зв’язків (trophic interaction strength)? Одним із підходів можуть бути маніпуляції над трофічною мережею, наприклад, спостереження за зміною в чисельності жертви після штучної елімінації її хижака. Результати подібних експериментів можна використати для обчислення різноманітних індексів інтенсивності зв’язків (Mittelbach & McGill 2019 Table 10.1). Звісно, подібні експерименти вимагають чималого людського й фінансового ресурсу і для складних трофічних мереж є недосяжними. Для результатів спостережень інтенсивність зв’язків можна оцінити як \[\frac{\Delta m_j \cdot p_{ij}}{m_i}\] де \(\Delta m_j\) є щоденною кількістю їжі, що споживає хижак (в одиницях ваги хижака, тобто \(\Delta m_j = 2\) позначатиме, що хижак з’їдає дві власні ваги на день), \(p_{ij}\) – пропорція жертви \(i\) в раціоні хижака \(j\), та \(m_i\) – біомаса жертви \(i\) (Bascompte et al. 2005).↩︎